Floyed 算法

同样是求最短路径，动态规划思想

区别：

• Dijsktra算法是求一个顶点到其他所有顶点的最短路径
• Floyed算法是求每个顶点到其他顶点的最短路径

思想：迭代两个表，一个距离的二阶矩阵，一个前驱结点的二阶矩阵

​ 若通过中间结点的距离小于直连的距离，则更新

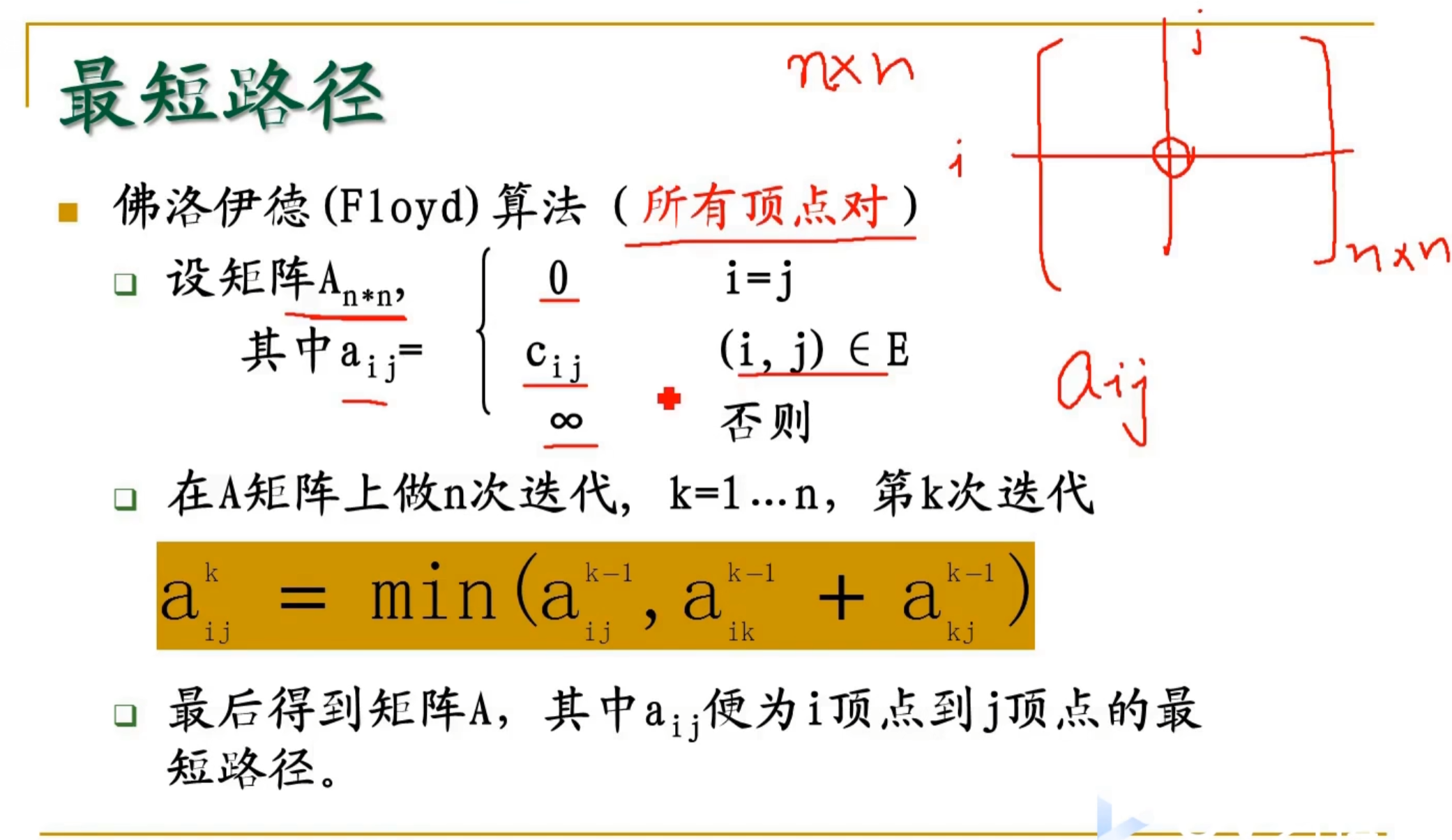
讲解：https://www.bilibili.com/video/BV1LE411R7CS/?spm_id_from=333.788.recommend_more_video.2&vd_source=1a7c0e12ae4c11965d82c6b8edcbdf0f

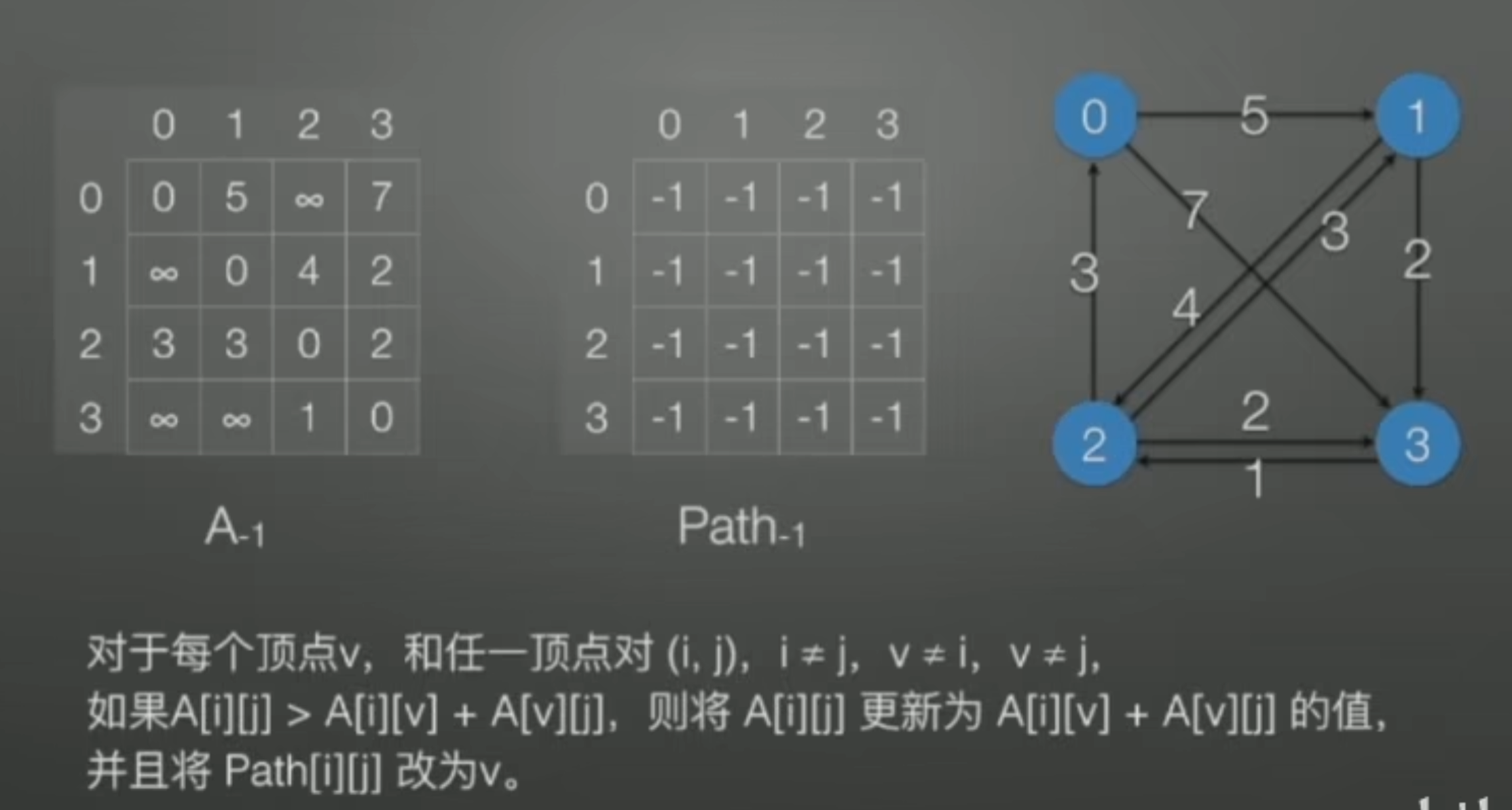
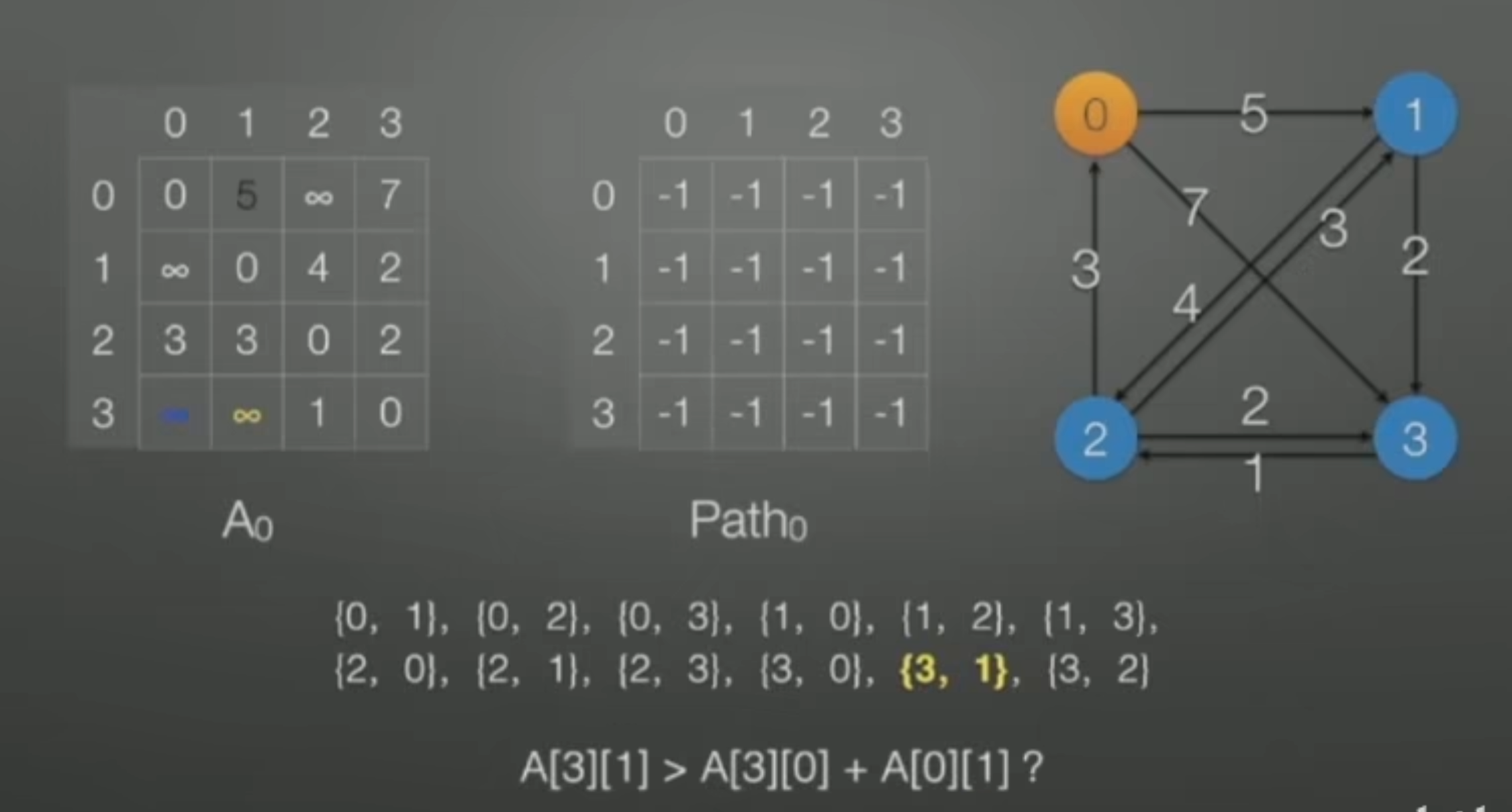
如果v=0：经过0这个顶点，更新6个顶点对（12个-所有带0的）

如果v=1：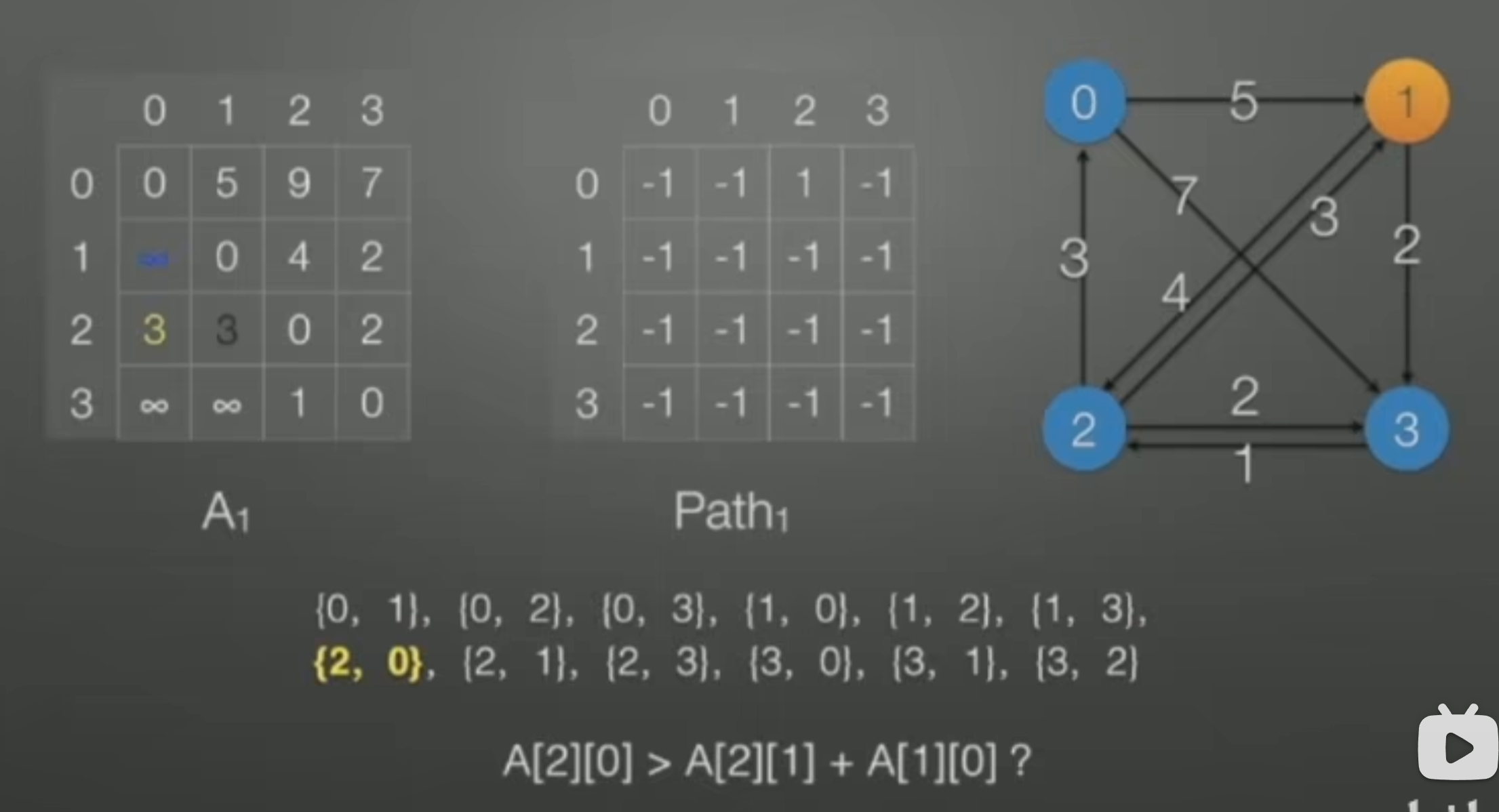

最后比如求从1到0的最短路径：-1表示有直接边相邻

public class FloyedDemo {

	public static void main(String[] args) {
		char[] vertex = new char[] {'A','B','C','D','E','F','G'};
		int[][] matrix = new int[vertex.length][vertex.length];
		final int N = 65535;
		matrix[0] = new int[]{0,5,7,N,N,N,2};
		matrix[1] = new int[]{5,0,N,9,N,N,3};
		matrix[2] = new int[]{7,N,0,N,8,N,N};
		matrix[3] = new int[]{N,9,N,0,N,4,N};
		matrix[4] = new int[]{N,N,8,N,0,5,4};
		matrix[5] = new int[]{N,N,N,4,5,0,6};
		matrix[6] = new int[]{2,3,N,N,4,6,0};
		Graph graph = new Graph(vertex, matrix);
		graph.floyed();
		graph.show();

	}

}
class Graph{
	public char[] vertex;
	public int[][] distance;//距离
	public int[][] pre;//前驱结点
	public Graph(char[] vertex, int[][] distance) {
		this.vertex = vertex;
		this.distance = distance;
		//初始化前驱结点
		pre = new int[vertex.length][vertex.length];
		for(int i = 0;i < vertex.length; i++) {
			for(int j = 0; j < vertex.length; j++) {
				pre[i][j] = i;
			}
		}
	}
	
	public void show() {
		System.out.println("distance: ");
		for(int i = 0;i < vertex.length; i++) {
			for(int j = 0; j < vertex.length; j++) {
				System.out.printf("%10d", distance[i][j]);
			}
			System.out.println();
		}
		System.out.println("pre: ");
		for(int i = 0;i < vertex.length; i++) {
			for(int j = 0; j < vertex.length; j++) {
				System.out.print(vertex[pre[i][j]] + "  ");
			}
			System.out.println();
		}
	}
	//floyed算法实现
	public void floyed() {
		int len = 65535;
		//k为中间结点
		for(int k = 0; k < vertex.length;k++) {
			//i为出发顶点
			for(int i = 0; i < vertex.length ;i++) {
				//j为到达顶点
				for(int j = 0; j < vertex.length ;j++) {
					len = distance[i][k] + distance[k][j];
					//如果经过中间顶点的路径更短的话，更新数组
					if(len < distance[i][j]) {
						distance[i][j] = len;//更新距离
						pre[i][j] = pre[k][j];//更新前驱结点
					}
					
				}
			}
		}
	}
}