Dijkstra算法

求图中两个节点之间最短路径问题：贪婪思想，路径必须是正数，如果是负数用Bellman-Ford算法

1. 求最短路径
2. 底层使用广度优先算法
3. 有三个集合要用：

• 记录被访问过的顶点
• 记录该顶点到起始点的最短路径
• 记录该路径的前驱结点

图解： https://www.bilibili.com/video/BV1zz4y1m7Nq/?share_source=copy_web&share_times=1&vd_source=1a7c0e12ae4c11965d82c6b8edcbdf0f

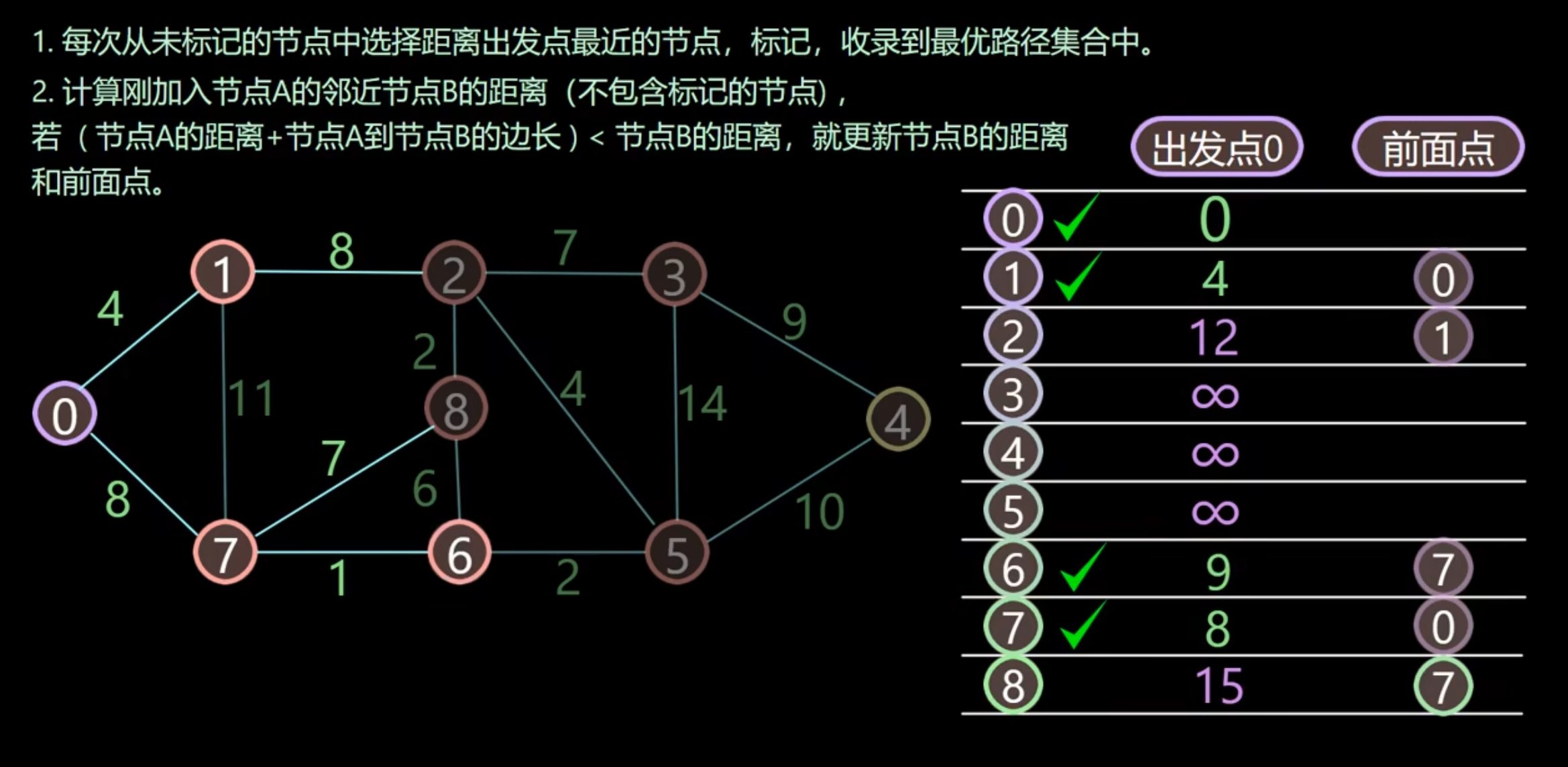
核心思想：选取最近节点，广度优先更新周围节点，再选取最近节点，以此类推

import java.util.Arrays;

public class DijkstraDemo {

	public static void main(String[] args) {
		char[] vertex = new char[] {'A','B','C','D','E','F','G'};
		int[][] matrix = new int[vertex.length][vertex.length];
		final int N = 65535;
		matrix[0] = new int[]{N,5,7,N,N,N,2};
		matrix[1] = new int[]{5,N,N,9,N,N,3};
		matrix[2] = new int[]{7,N,N,N,8,N,N};
		matrix[3] = new int[]{N,9,N,N,N,4,N};
		matrix[4] = new int[]{N,N,8,N,N,5,4};
		matrix[5] = new int[]{N,N,N,4,5,N,6};
		matrix[6] = new int[]{2,3,N,N,4,6,N};
		Graph graph = new Graph(vertex, matrix);
		graph.dijkstra(6);
		

	}

}

class Graph{
	public char[] vertex;
	public int[][] matrix;
	public VisitedVertex vv;
	public Graph(char[] vertex, int[][] matrix) {
		super();
		this.vertex = vertex;
		this.matrix = matrix;
	}
	public void showGraph() {
		for(int i = 0; i < vertex.length; i++) {
			for(int j = 0; j < vertex.length; j++) {
				System.out.printf("%10d", matrix[i][j]);
			}
			System.out.println();
		}
	}
	//算法，先更新开始节点
	public void dijkstra(int index) {
		vv = new VisitedVertex(vertex.length, index);
		update(index);
		for(int i = 0; i < vertex.length;i++) {
			index = vv.nextVertex();
			update(index);
		}
		
		//输出
		System.out.println("distance");
		for(int i : vv.distance) {
			System.out.print(i + "  ");
		}
		System.out.println("pre");
		for(int i : vv.pre) {
			System.out.print(i + "  ");
		}
	}
	//访问某个点之后的更新
	public void update(int index) {
		int len = 0;
		//广度遍历
		for(int i = 0; i < matrix[index].length;i++) {
			//距离增加
			len = matrix[index][i] + vv.distance[index];
			//更新距离,前驱结点
			if(vv.isVisited[i] == 0 && len < vv.distance[i]) {
				vv.distance[i] = len;
				vv.pre[i] = index;
			}
		}
		
	}
	
}
//已访问过的顶点的信息
class VisitedVertex{
	//记录顶点是否被访问过
	public int isVisited[];
	//值为该节点的前驱结点，会动态更新
	public int pre[];
	//值为出发顶点到其他所有顶点的距离
	public int distance[];
	//构造
	public VisitedVertex(int length, int index) {
		isVisited = new int[length];
		isVisited[index] = 1;
		pre = new int[length];
		Arrays.fill(pre, -1);
		distance = new int[length];
		Arrays.fill(distance, 65535);
		distance[index] = 0;
	}
	//下一个要访问的节点
	public int nextVertex() {
		int min = 65536;
		int index = 0;
		for(int i = 0; i < isVisited.length; i++) {
			if(isVisited[i] == 0 && distance[i] < min) {
				min = distance[i];
				index = i;
			}
		}
		isVisited[index] = 1;
		return index;
	}
}