kruscal算法

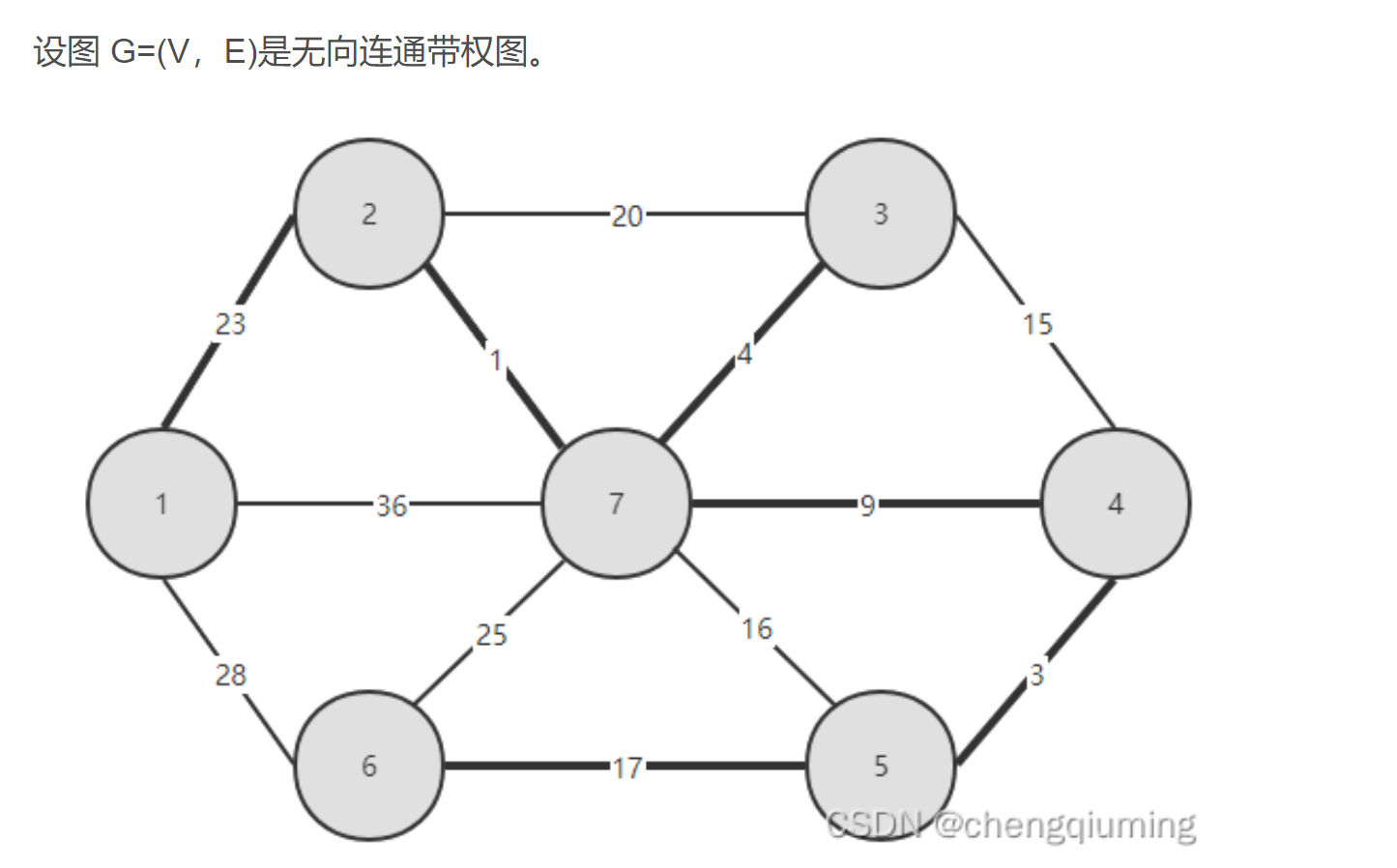
也是求最小生成树（适合求稀疏的网）

思路：按照权值大小选择n-1条边，并保证不构成回路

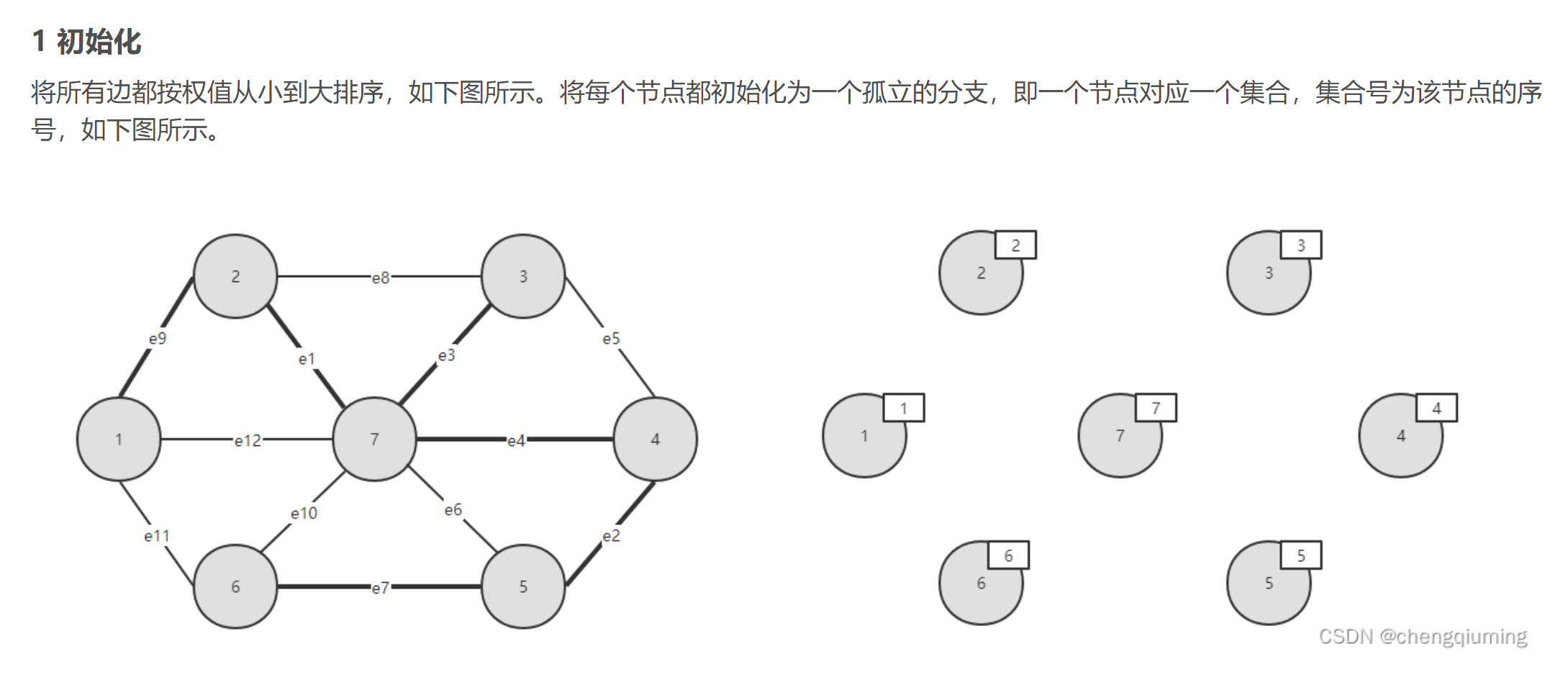
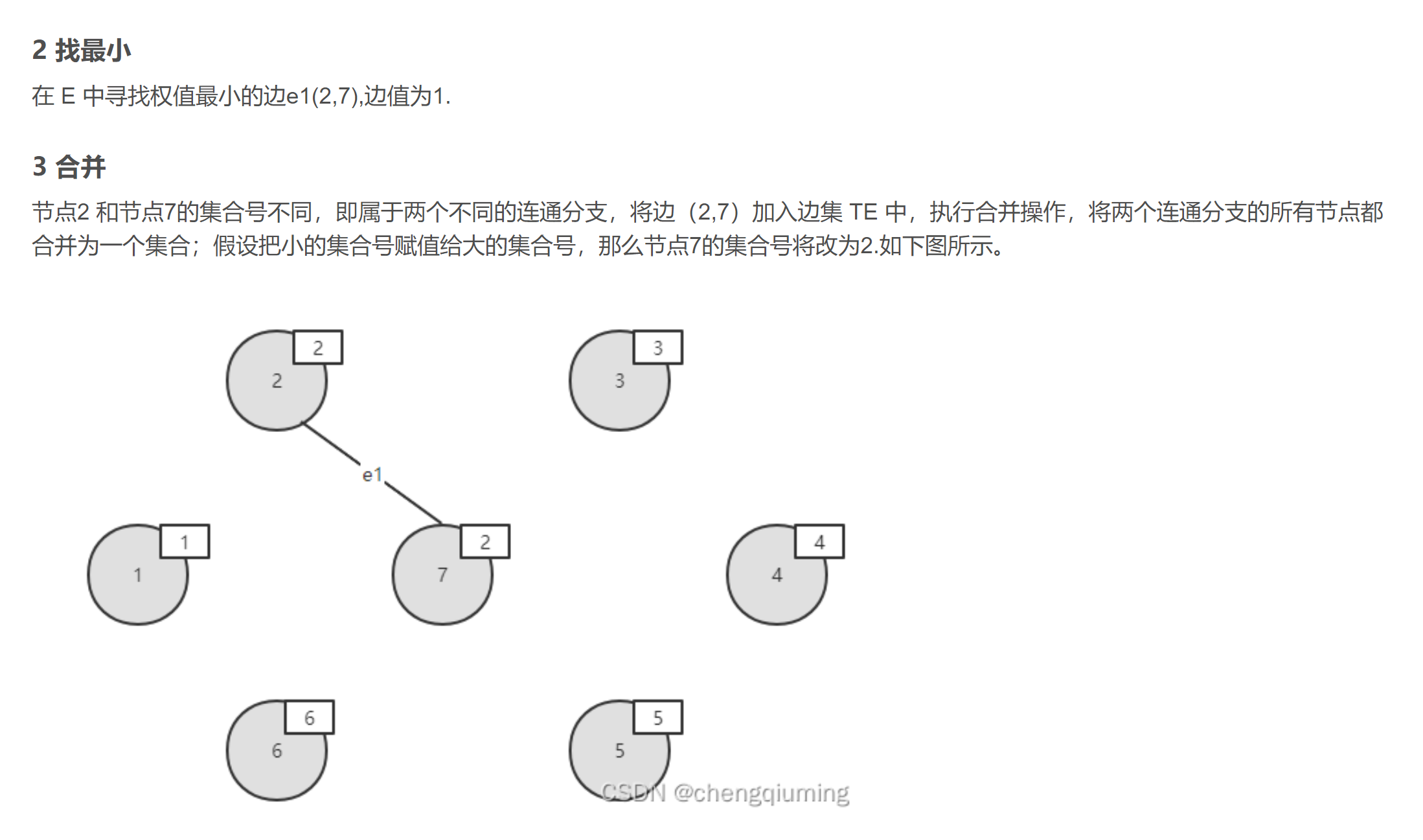
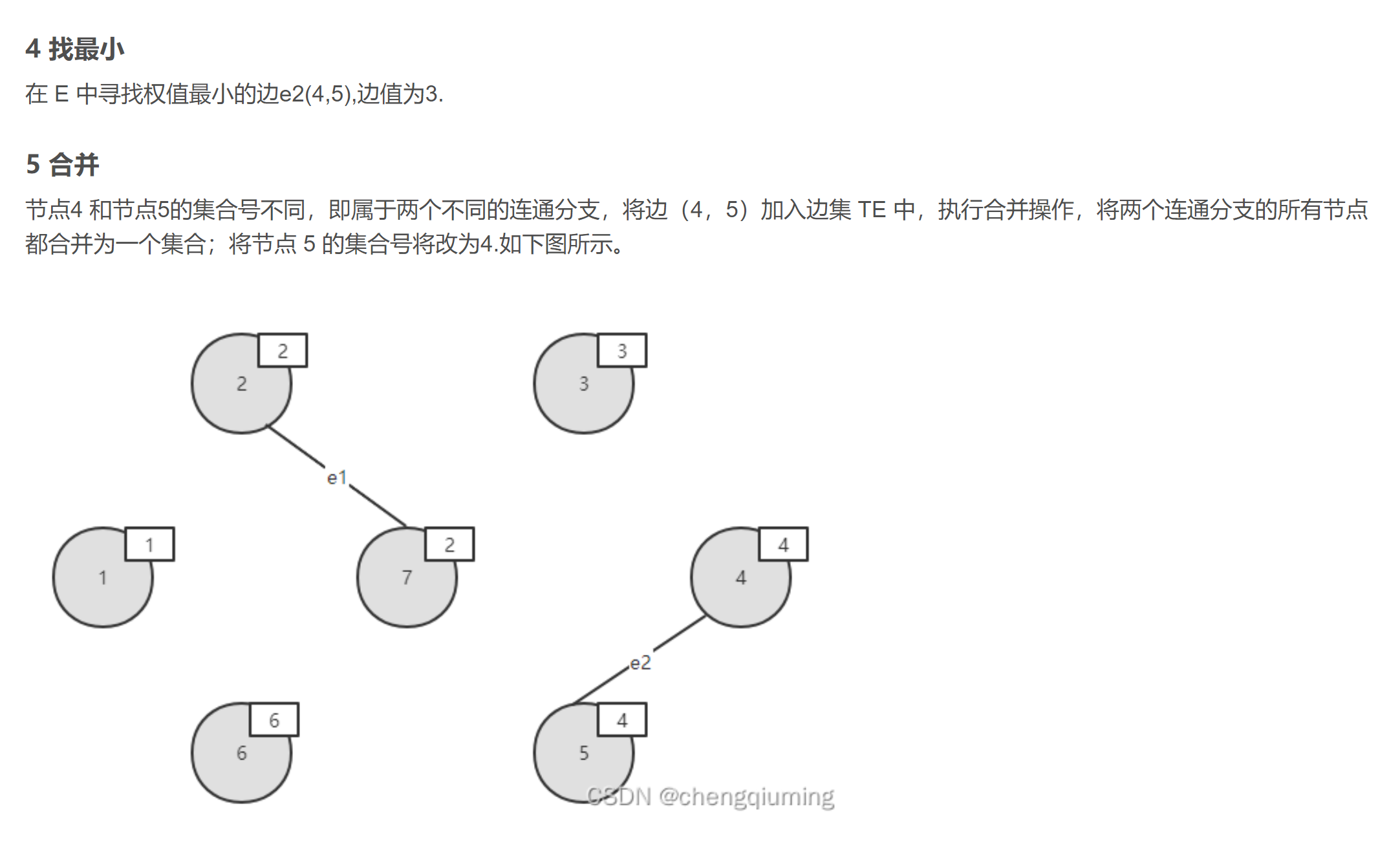
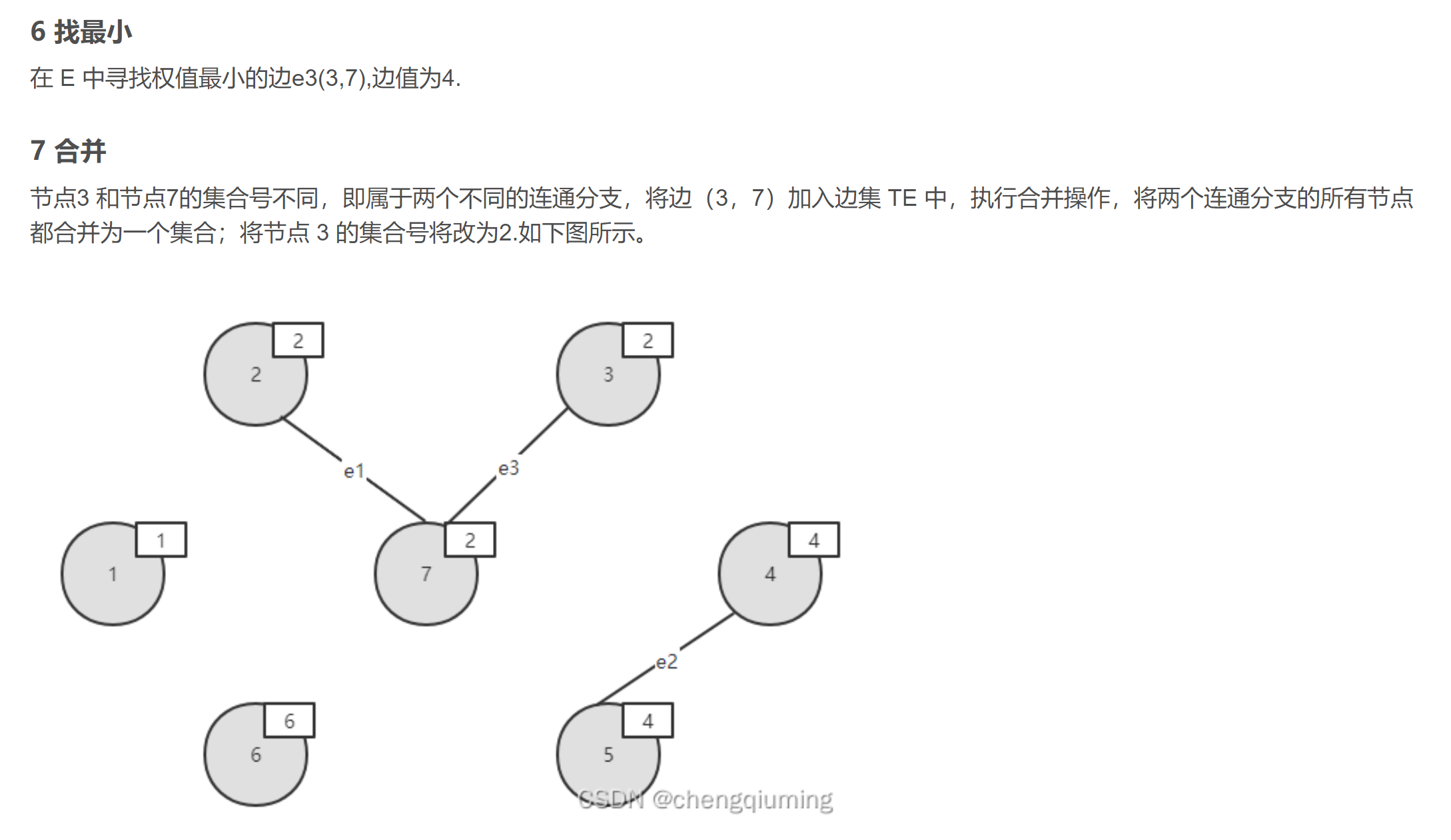
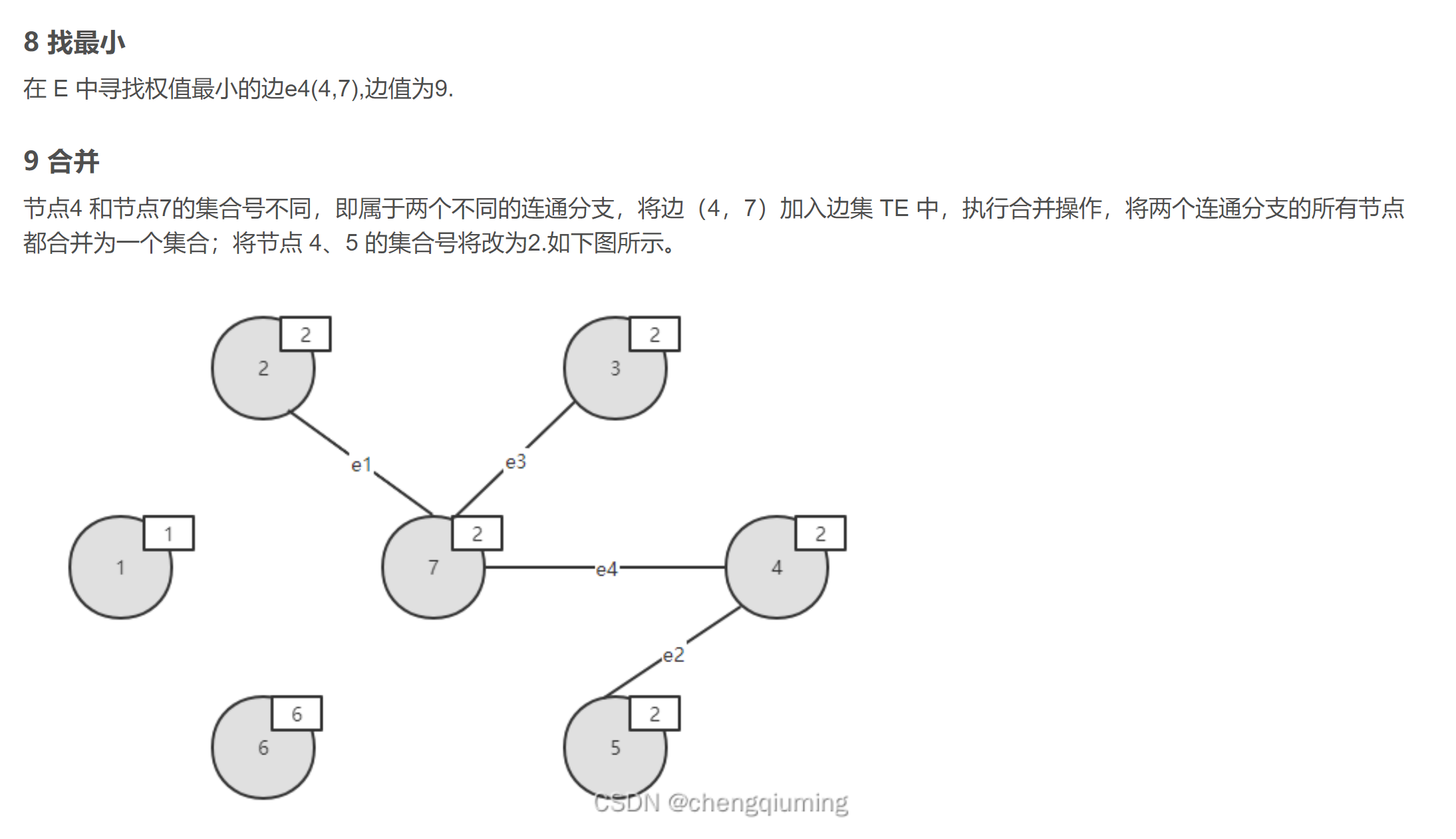
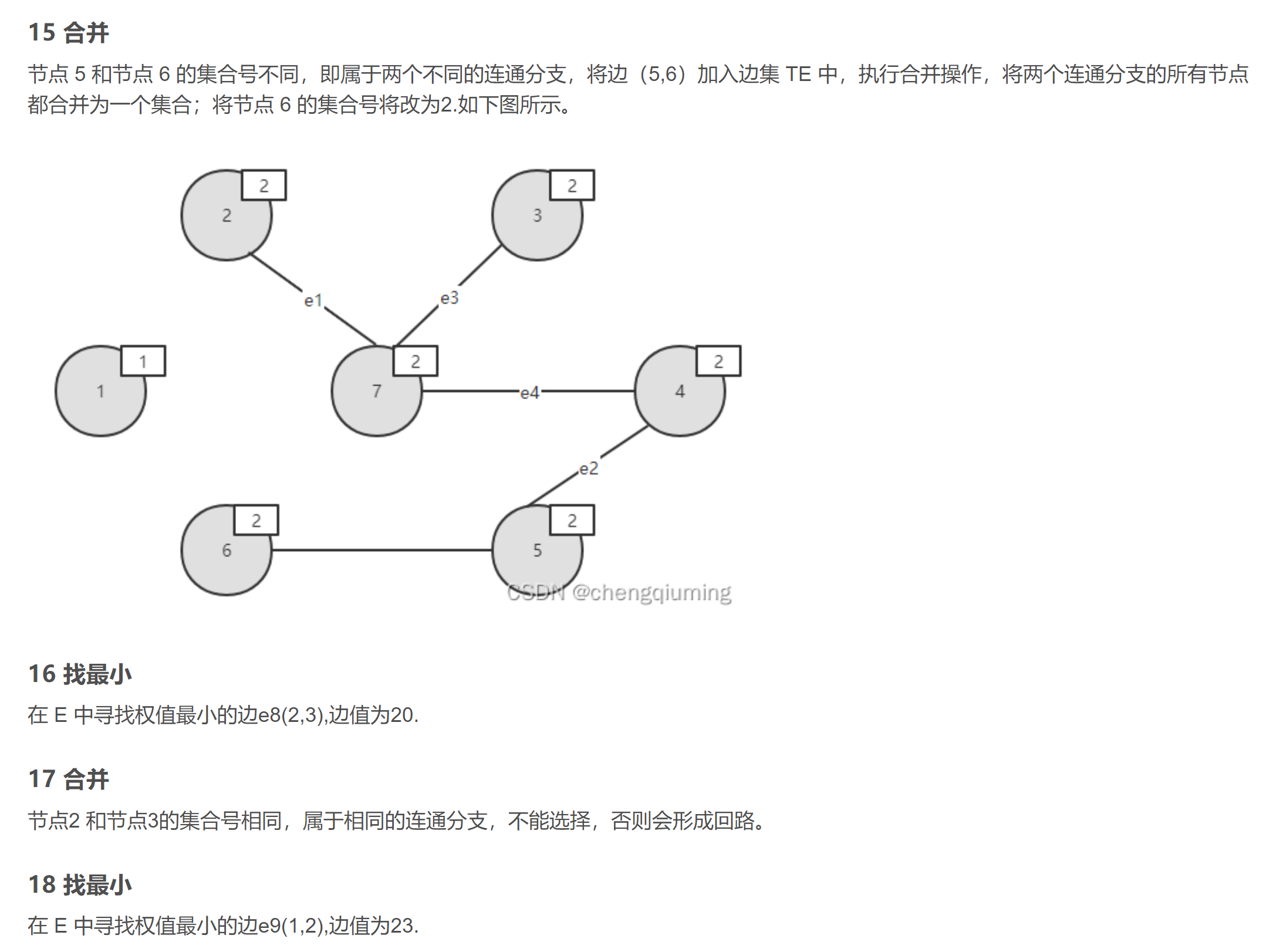
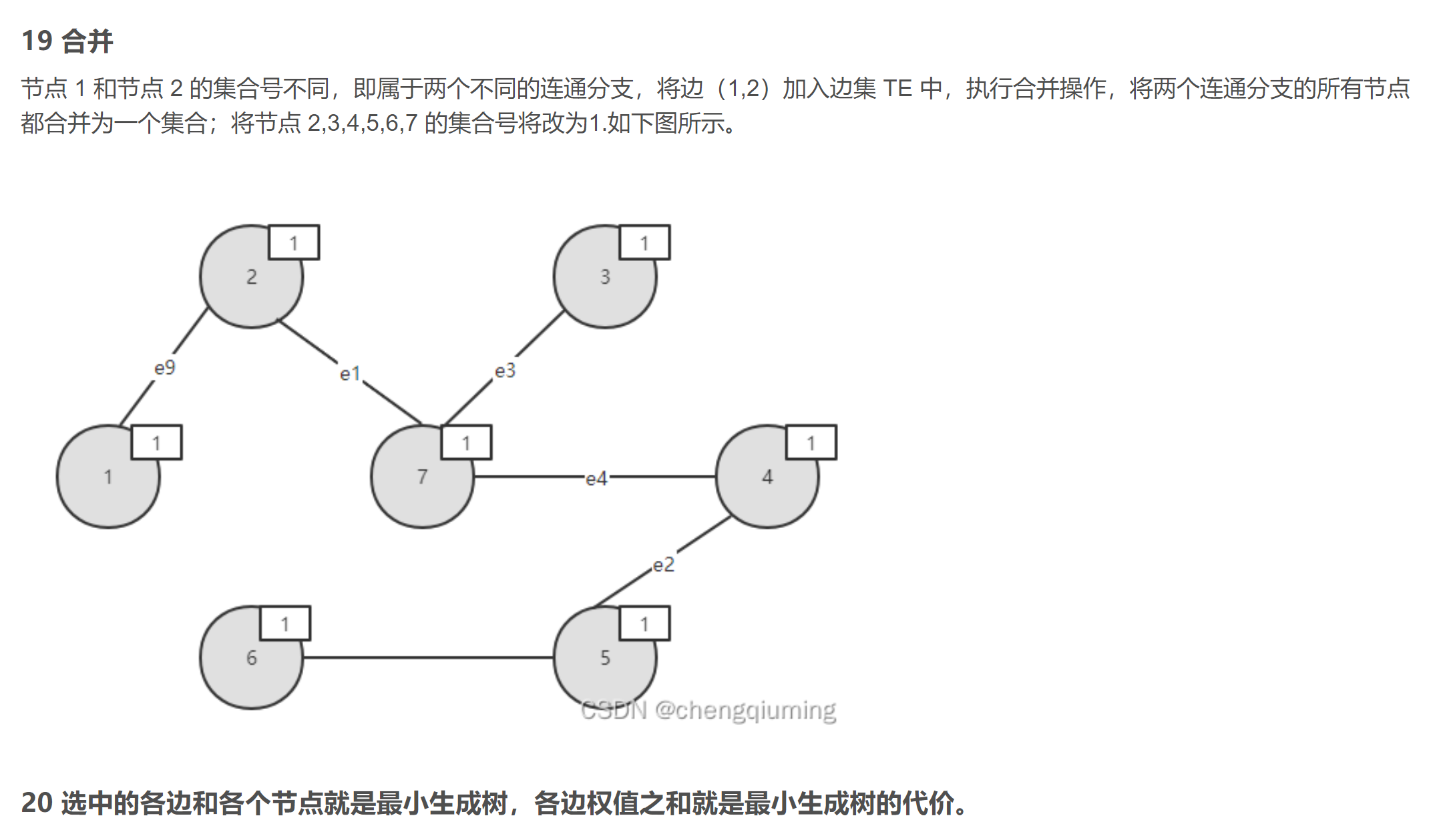
1.排序

2.判断是否构成回路

• 某个顶点的终点：把顶点排好后，与它连通的最大顶点，也就是标记同一棵树
• 终点相同的两个顶点不能连起来，否则会构成回路

import java.util.Arrays;


public class KruskalDemo {
	public static int INF = Integer.MAX_VALUE;
	public int edgenum = 0;//边的数量
	public int num;//节点的数量
	public char[] vertex;//顶点信息
	public int[][] weight;//边的权值，邻阶矩阵
	//存放边的数组
	public Edge[] edges;
	//存放结果数组
	public Edge[] results;
	//存放终点
	public int[] end;
	public KruskalDemo(int num, char[] vertex, int[][] weight) {
		this.num = num;
		this.vertex = vertex;
		this.weight = weight;
		
		for(int i = 0; i < num; i++) {
			for(int j = i + 1; j < num;j++) {
				if(this.weight[i][j] != INF) {
					edgenum++;
				}
			}
		}
		
		edges = new Edge[edgenum];
		results = new Edge[edgenum];
		end = new int[num];
		//把邻阶矩阵转换到边的集合里
		int m = 0;
		for(int i = 0; i < num; i++) {
			for(int j = i + 1; j < num;j++) {
				if(weight[i][j] != INF) edges[m++] = new Edge(i, j, weight[i][j]);
			}
		}
	}
	
	public void showGraph() {
		for(int i = 0; i < num;i++) {
			for(int j = 0; j < num;j++) {
			System.out.printf("%15d", weight[i][j]);
			}
			System.out.println();
		}
	}
	//对边进行排序
	public void sortEdge() {
		Arrays.sort(edges);
	}
	//获取某个顶点的终点
	public int getEnd(int vertex) {
		while(end[vertex] != 0) {
			vertex = end[vertex];
		}
		return vertex;
	}
	public void kruscal() {
		int index = 0;

		//1.对边进行排序
		this.sortEdge();
		//2.判断是否存在回路：看终点是否一样
		for(int i = 0; i < edgenum; i++) {
			int v1 = edges[i].v1;
			int v2 = edges[i].v2;
			int end1 = this.getEnd(v1);
			int end2 = this.getEnd(v2);
			if(end1 != end2) {
				results[index++] = edges[i];
				end[end1] = end2;
			}
			
			//输出
			for(int j: end) {
				System.out.print(j + " ");
			}
			System.out.println();
		}
		
		
	}

	public static void main(String[] args) {
		int num = 5;
		char[] vertex = new char[] {'A', 'B', 'C', 'D', 'E'};
		int[][] weight = new int[][] {
		    { 0, 5, INF, 8, 10 }, 
			{ 5, 0, 2, INF, 6 }, 
			{ INF, 2, 0, 3, INF },
			{ 8, INF, 3, 0, INF }, 
			{ 10, 6, INF, INF, 0 } 
		};
		KruskalDemo kruskal = new KruskalDemo(num, vertex, weight);
		kruskal.kruscal();

		for(Edge i: kruskal.results) {
			System.out.println(i);
		}
		for(int i = 0; i < kruskal.num; i++) {
			System.out.println(kruskal.getEnd(i));
		}
		
	}

}
//边的类
class Edge implements Comparable<Edge>{
	public int v1;
	public int v2;
	public int weight;
	public Edge(int v1, int v2, int weight) {
		super();
		this.v1 = v1;
		this.v2 = v2;
		this.weight = weight;
	}
	@Override
	public String toString() {
		return "Edge [v1=" + v1 + ", v2=" + v2 + ", weight=" + weight + "]";
	}
	@Override
	public int compareTo(Edge o) {
		if(this.weight < o.weight) return -1;
		else if(this.weight > o.weight) return 1;
		else {
			return 0;
		}
	}
	
}