Prime算法

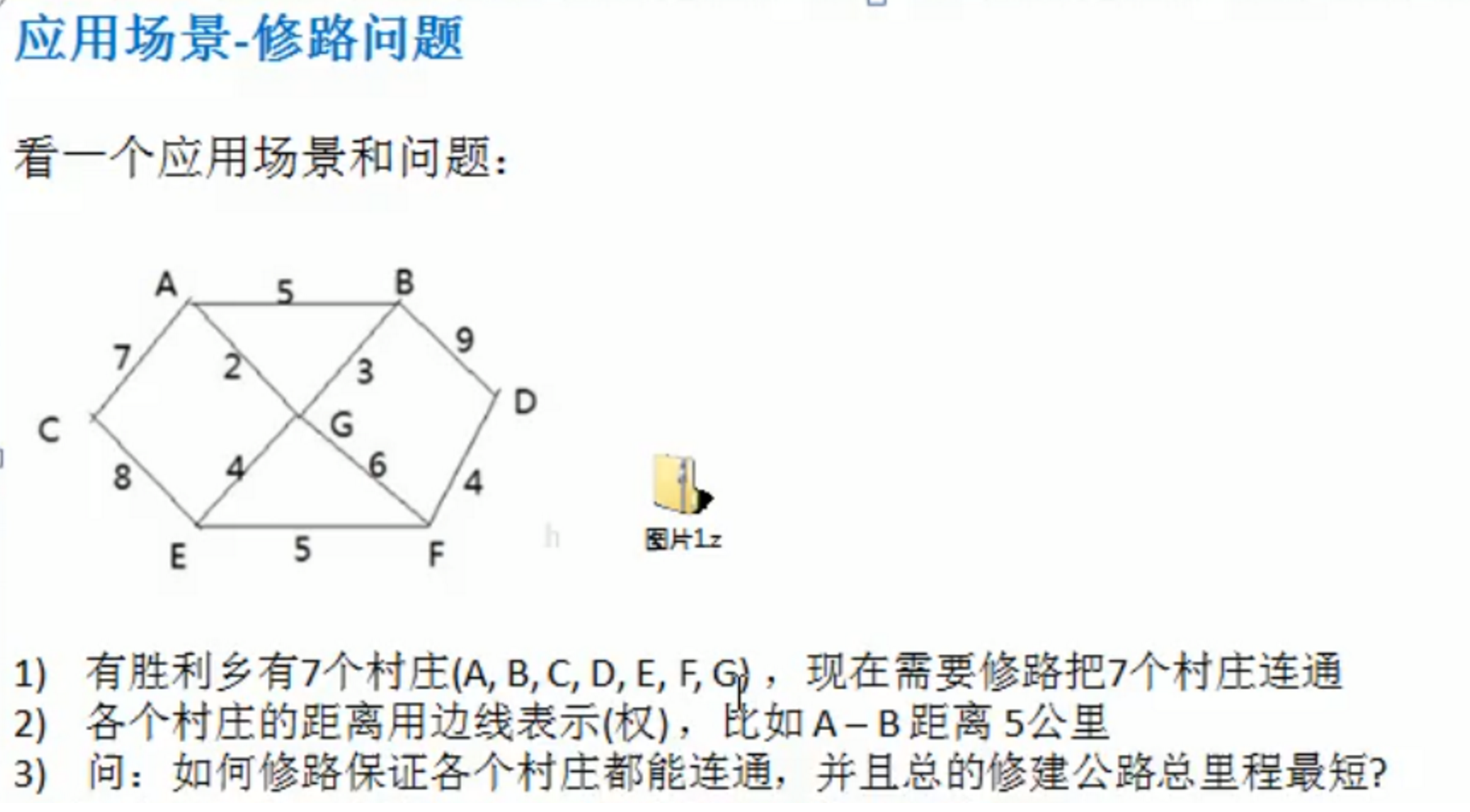
也就是求最小生成树（适合边的稠密度高的网）

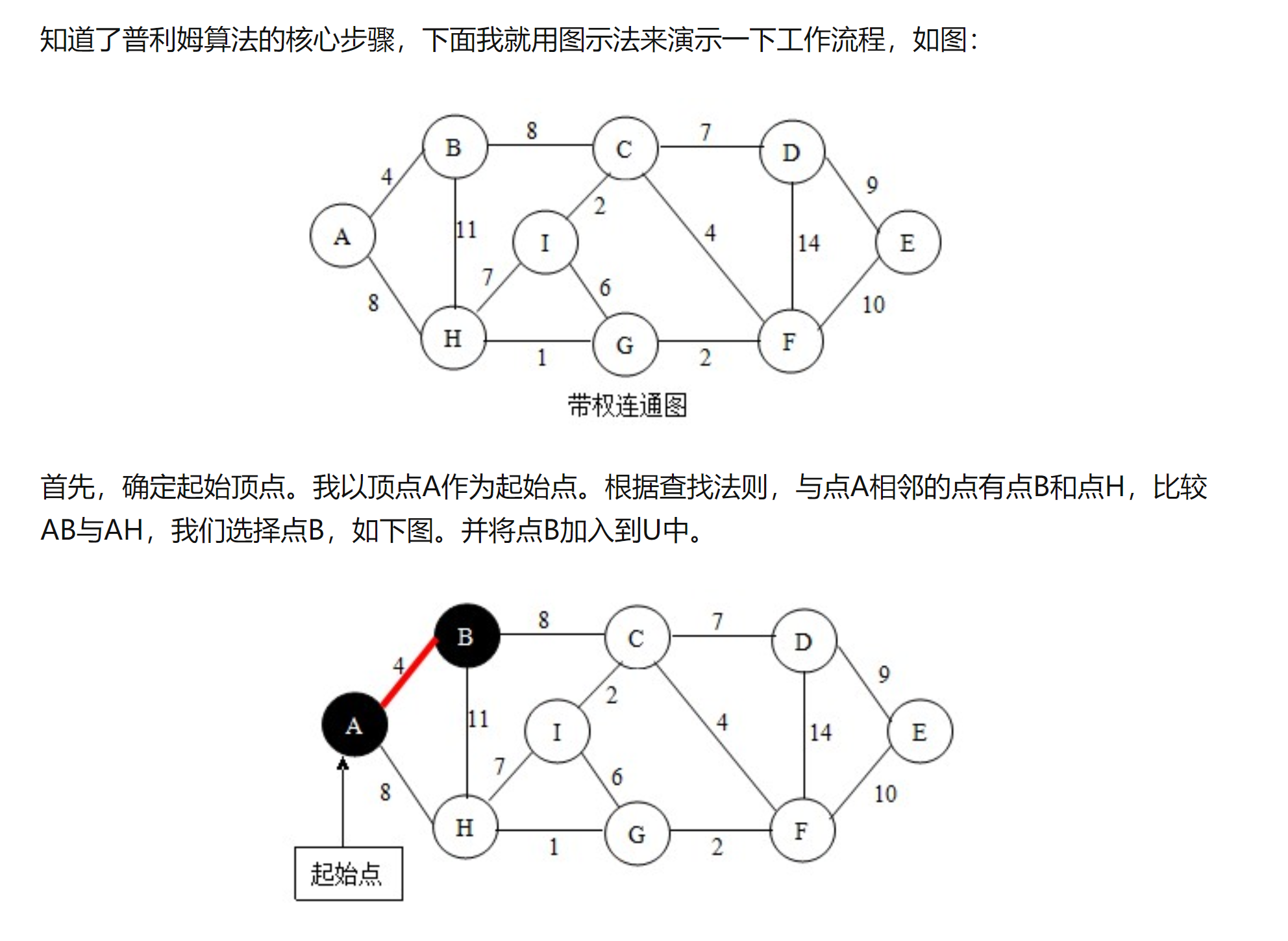
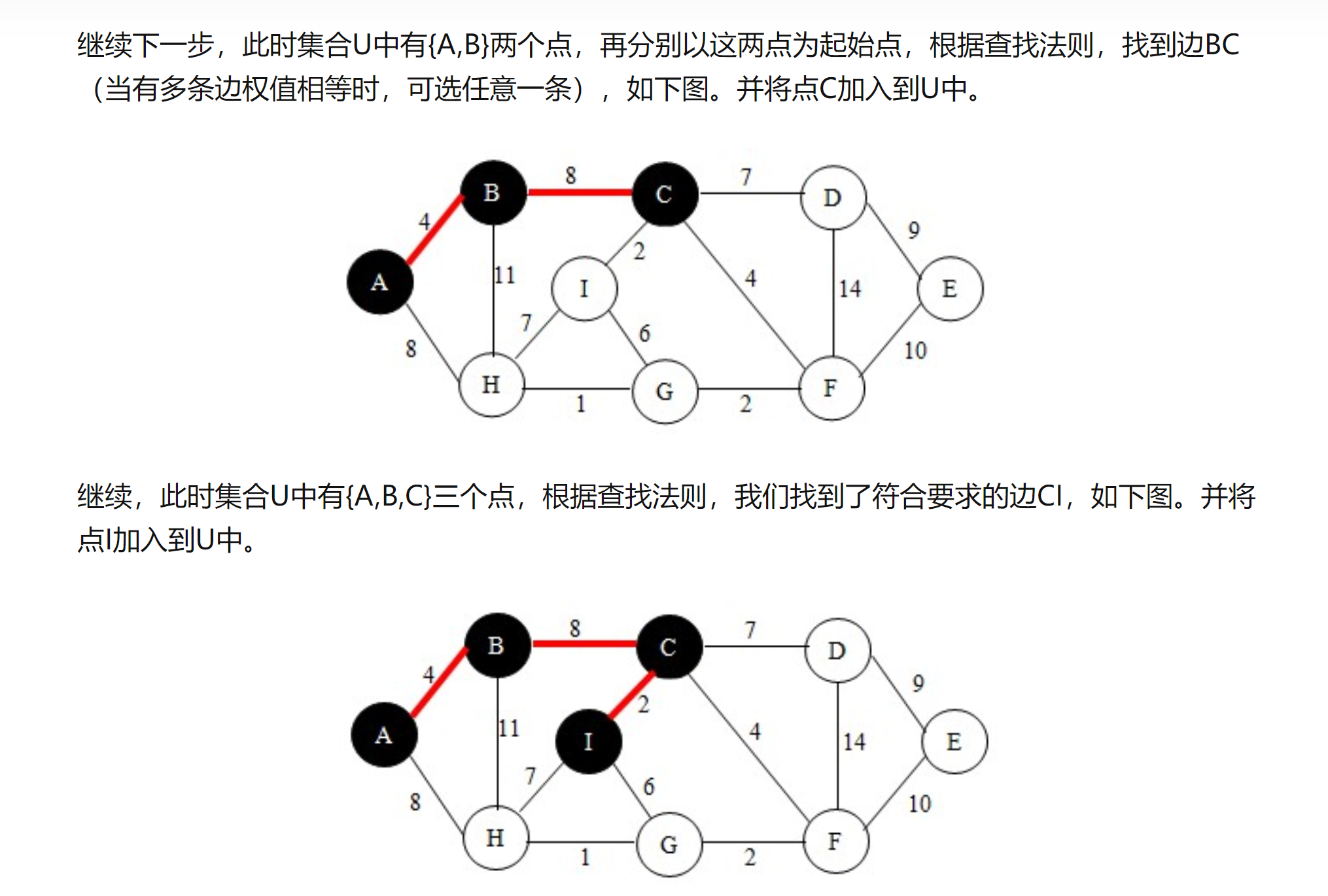
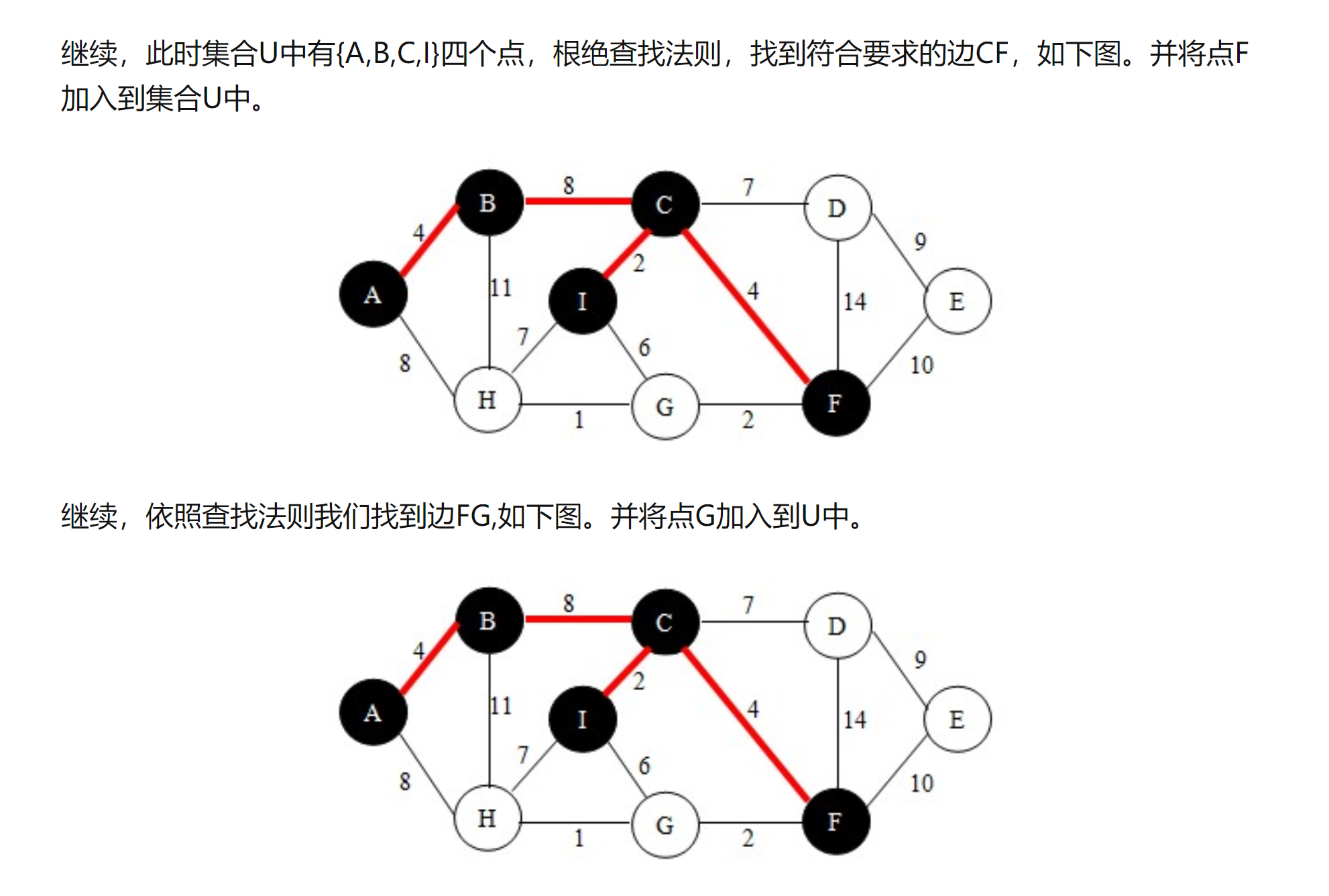
思路：从初始节点开始，寻找最短路径，生成最小生成树，然后根据树，寻找最短路径

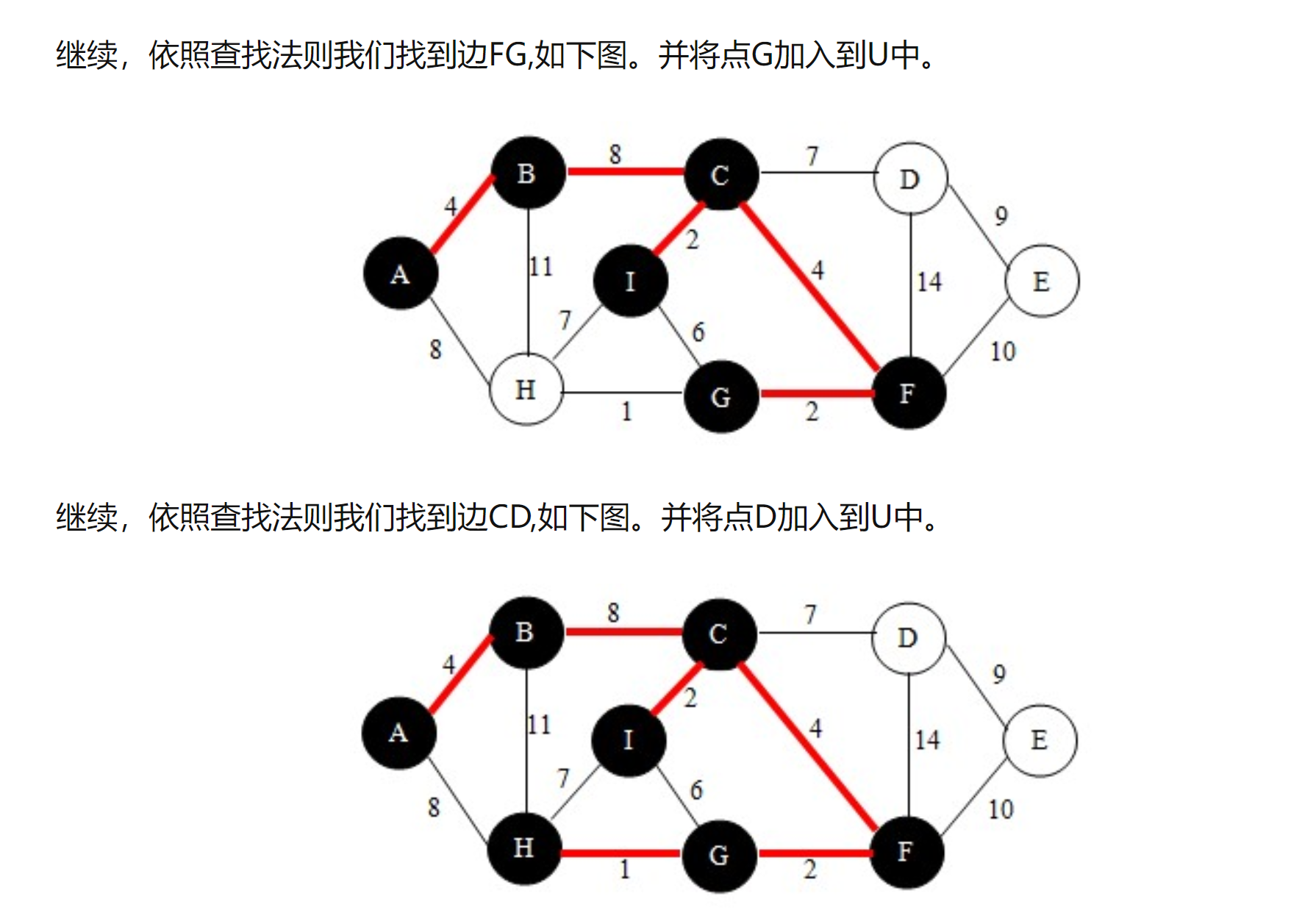
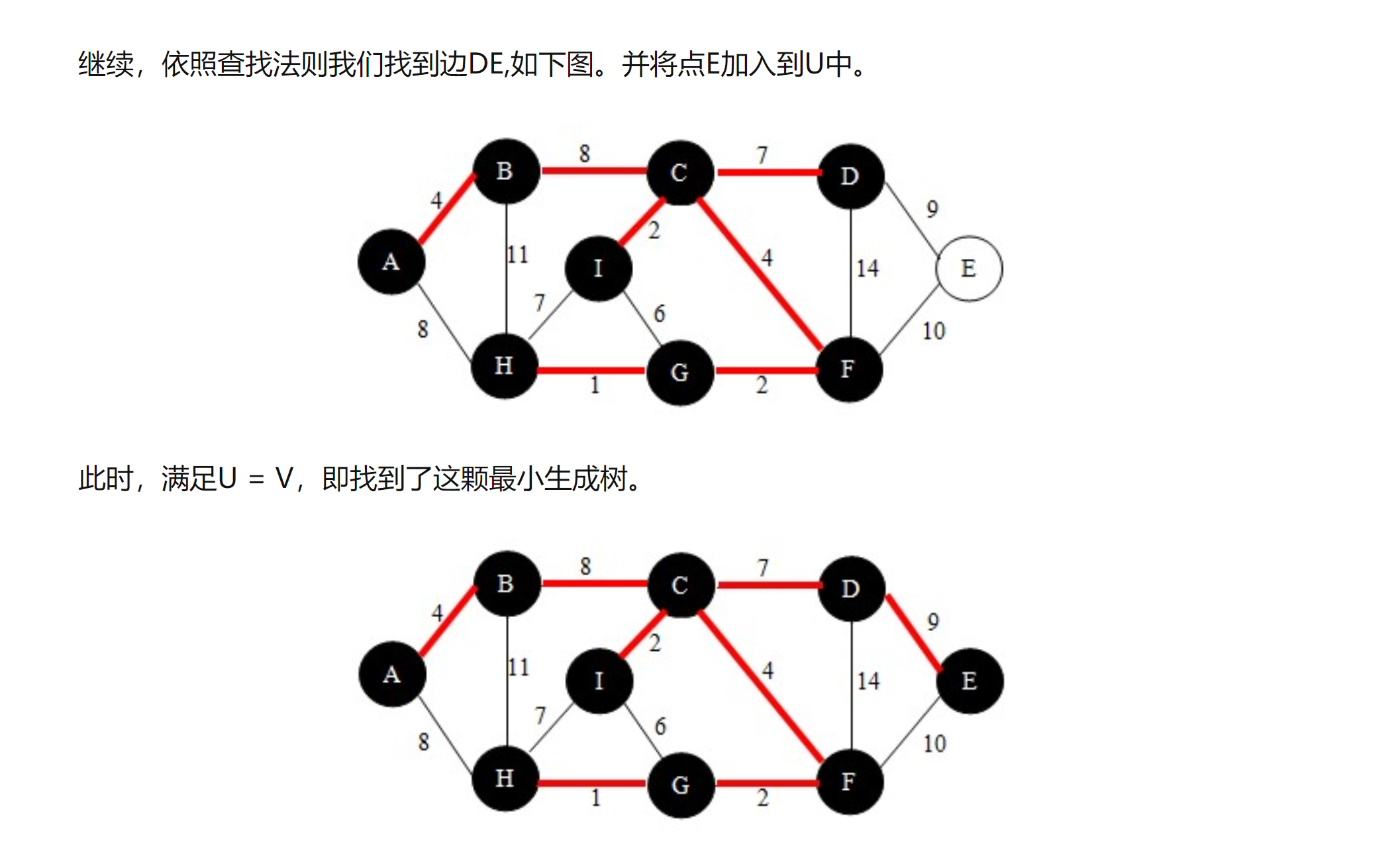
import java.util.Arrays;

public class PrimeDemo {

	public static void main(String[] args) {
		MinTree min = new MinTree();
		char[] vertex = new char[] { 'A', 'B', 'C', 'D', 'E' };
		int[][] weight = new int[][] { { 9999, 5, 9999, 8, 10 }, { 5, 9999, 2, 9999, 6 }, { 9999, 2, 9999, 3, 9999 },
				{ 8, 9999, 3, 9999, 9999 }, { 10, 6, 9999, 9999, 9999 } };
		Graph graph = new Graph(5);
		min.createGraph(graph, 5, vertex, weight);
		min.showGraph(graph);
		min.prime(graph, 2);

	}

}

class MinTree {
	// 创建一个图
	public void createGraph(Graph graph, int num, char[] vertex, int[][] weight) {
		for (int i = 0; i < vertex.length; i++) {
			graph.vertex[i] = vertex[i];
		}
		for (int i = 0; i < weight.length; i++) {
			for (int j = 0; j < weight[i].length; j++) {
				graph.weight[i][j] = weight[i][j];
			}
		}
	}

	// 输出图
	public void showGraph(Graph graph) {
		for (int[] i : graph.weight) {
			System.out.println(Arrays.toString(i));
		}
	}

	// prime
	/**
	 * prime算法实现
	 * 
	 * @param graph；图
	 * @param v：第一个遍历的顶点
	 */
	public void prime(Graph graph, int v) {
		// 记录总路径长度
		int sum = 0;
		int isVisited[] = new int[graph.num];
		isVisited[v] = 1;
		// 记录权值
		int min = 9999;
		// 记录两个点的下标
		int v1 = -1;
		int v2 = -1;
		// 存放最小的节点
		int m = -1;
		for(int j = 1; j < graph.num; j++) {//算法结束后，有num - 1条边
		//找到最小的节点的路径
		for (int i = 0; i < graph.num; i++) {
		    for (m = 0; m < graph.num; m++) {
		    	//m为即将被访问的
					if (isVisited[i] == 1 && isVisited[m] == 0 && graph.weight[i][m] < min) {
						min = graph.weight[i][m];
						v1 = i;
						v2 = m;
					}
				}
			}
			sum = sum + min;
			isVisited[v2] = 1;
			System.out.println(v1 + "----" + v2);
			min = 9999;
	}
		System.out.println("sum = " + sum);
		}
}

class Graph {
	public int num;// 图的节点数量
	public char[] vertex;// 图节点的信息
	public int[][] weight;// 图的邻接矩阵
	// 初始化图

	public Graph(int num) {
		this.num = num;
		weight = new int[num][num];
		vertex = new char[num];
	}

}