DP 动态规划

动态规划：把一个大问题分解为若干个小问题求解，与分治算法不同的是，这几个问题之间关系，即一个问题是在另外一个问题的基础之上的。

背包问题：

• 背包容量固定，要往背包里放总价值最大的物品

• 分为01背包（每件物品只能放一次）完全背包（物品的数量为无限件）

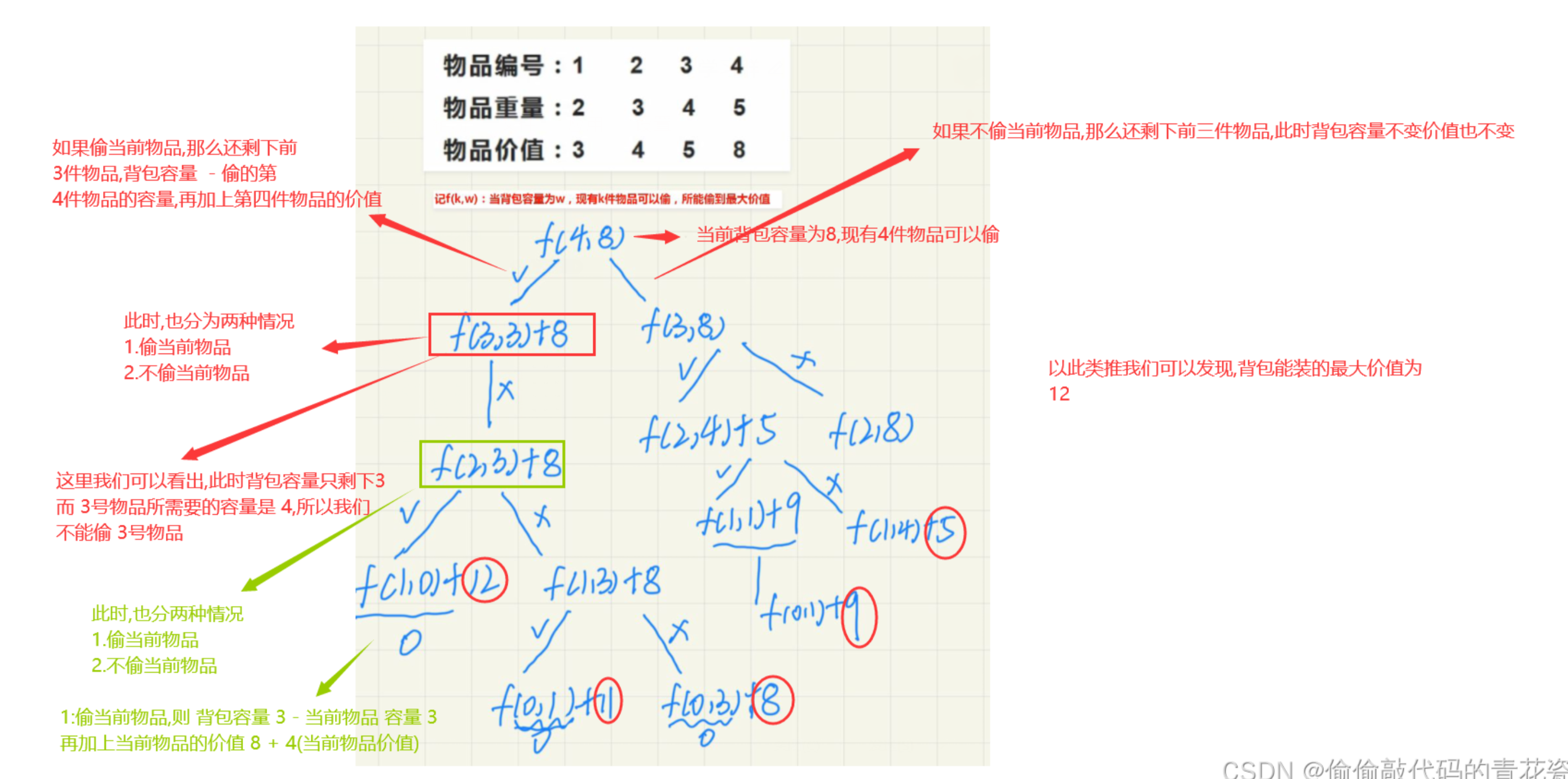
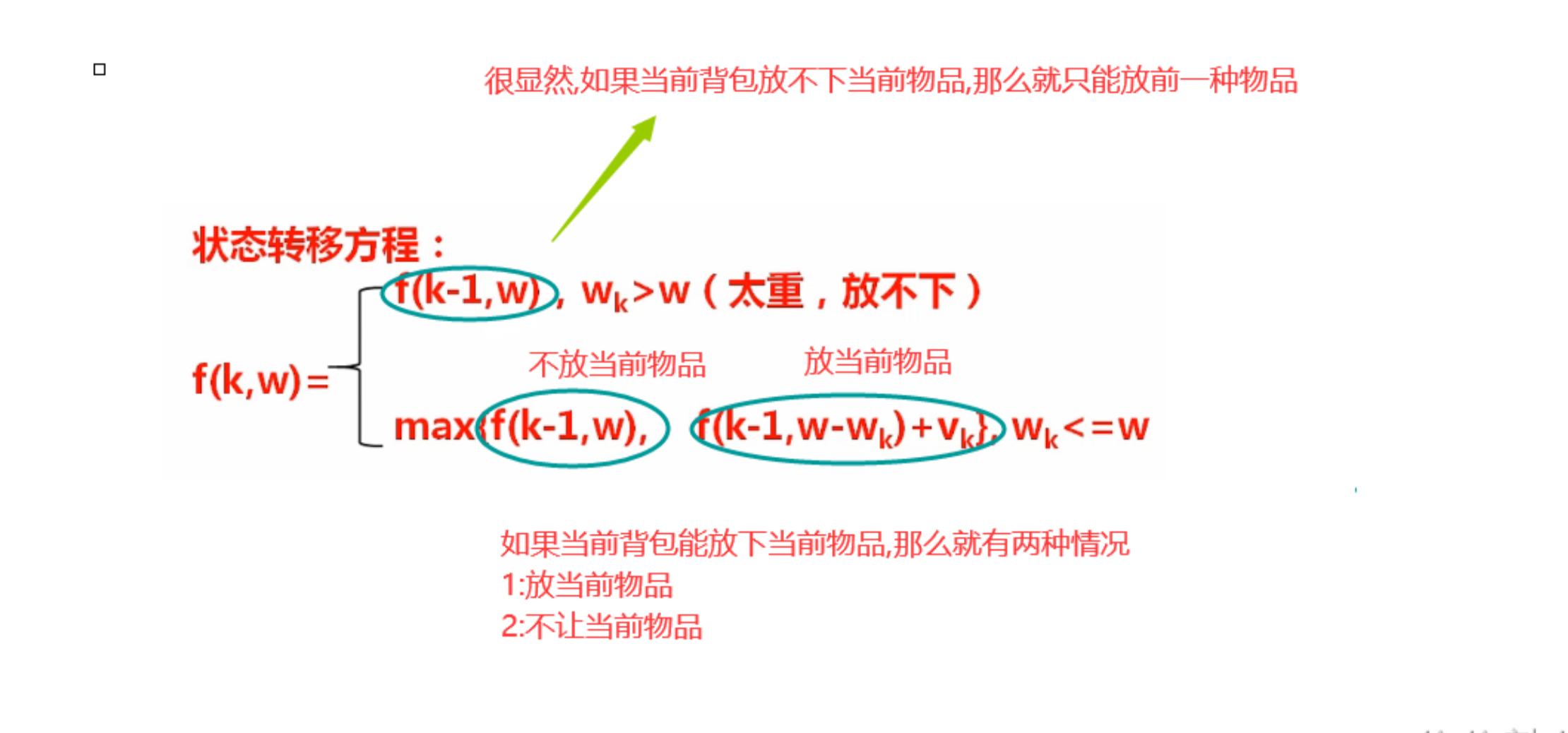
为了方便理解 这里 W代表物品的重量(背包容量),V代表物品的价值,f(k,w)代表:当背包容量为w,现有K件物品可以装,所能偷到的最大价值

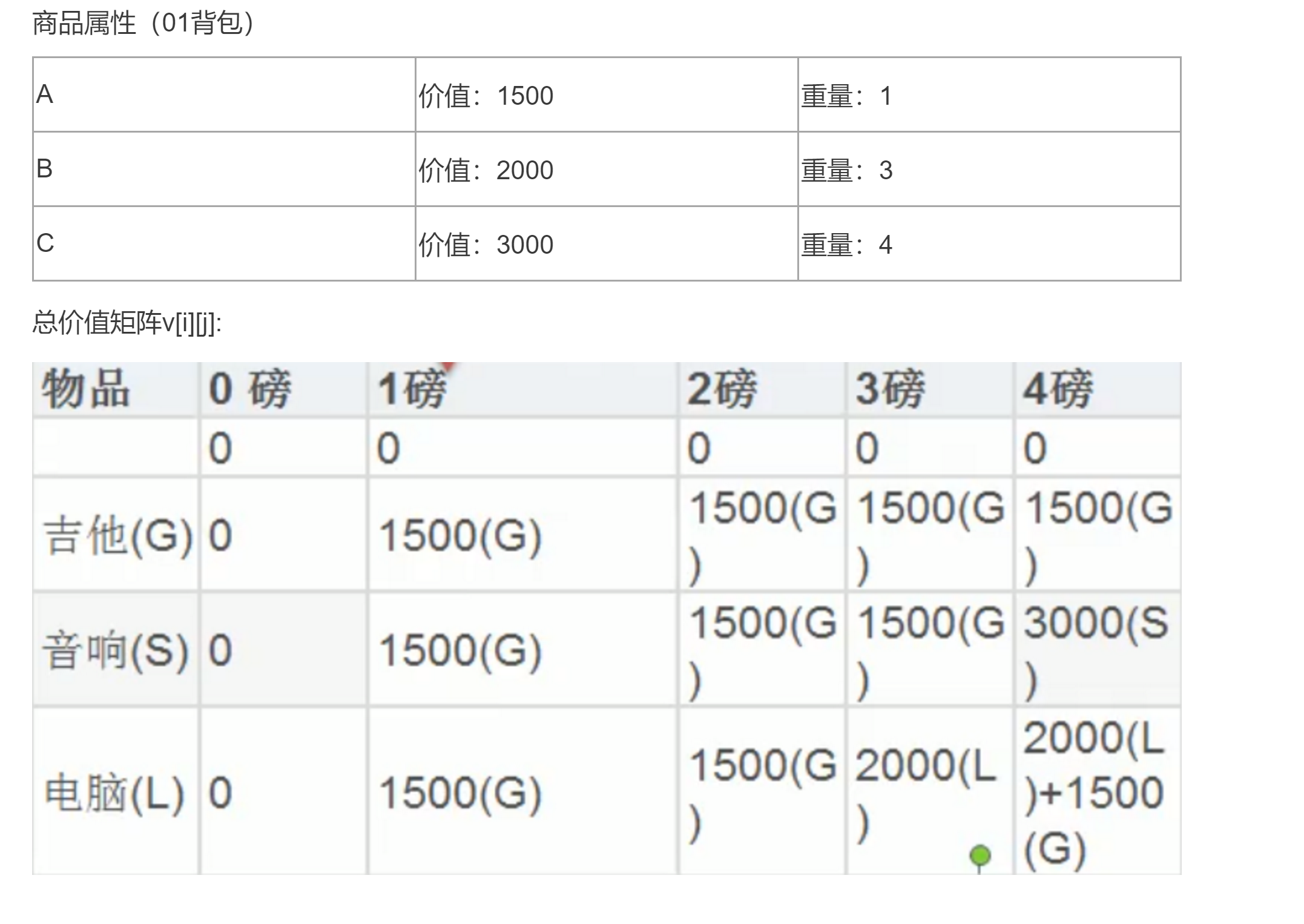
public class Knapsack {

	public static void main(String[] args) {
		int weight[]  = new int[] {1,4,3};//物品的重量
		int value[] = new int[] {1500,3000,2000};//物品的价值
		int pack = 4;//背包的容量
		int fin[][] = new int[weight.length + 1][pack + 1];
		int detail[][] = new int[weight.length + 1][pack + 1];
		//首先把第一行和第一列赋值为0
		for(int i = 0; i < weight.length + 1; i++) {
			fin[i][0] = 0;
		}
		for(int i = 0; i < pack + 1; i++) {
			fin[0][i] = 0;
		}
		
		
		for(int i = 1; i < weight.length + 1; i++ ) {
			for(int j = 1; j <= pack; j++) {
				//计算书包放不下的情况
				if(weight[i - 1] > j) {
					fin[i][j] = fin[i - 1][j];
				}
				//书包可以放下的情况
				else {
					//fin[i][j] = Math.max(fin[i - 1][j] ,value[i - 1] + fin[i - 1][j - weight[i - 1]]);
					if(fin[i - 1][j] < value[i - 1] + fin[i - 1][j - weight[i - 1]]) {
						fin[i][j] = value[i - 1] + fin[i - 1][j - weight[i - 1]];
						detail[i][j] = 1;
					}
					else {
						fin[i][j] = fin[i - 1][j];
					}
				}
			}
		}
		//输出
		for(int i[]: fin) {
			for(int j: i) {
				System.out.print(j + "  ");
			}
			System.out.println();
		}
		
		for(int i[]: detail) {
			for(int j: i) {
				System.out.print(j + "  ");
			}
			System.out.println();
		}
		int w = pack;
		int q = weight.length;
		while(w > 0) {
			if(detail[q][w] == 1) {
				System.out.println("第 " + q + "个");
				w = w - weight[q - 1];
			}
			
			
			q = q - 1;
		}
	
	

	}
}

推导： https://blog.csdn.net/sunqi568/article/details/81320364

动态规划问题汇总：

https://blog.csdn.net/Biteht/article/details/124298926?spm=1001.2014.3001.5501