Ch04 Search

线性查找

遍历数组，一个一个查找

二分查找

递归, 查找有序数组（如果要找出所有元素的下标可以用链表存起来）

public class DoubleFind {

	public static void main(String[] args) {
		int[] arr = new int[] {1,2,3,6,7,8,9};
		int result = doufin(arr, 4, 0, 6);
		System.out.println(result);

	}
	public static int doufin(int arr[], int target, int left, int right) {
		int mid = (left + right) / 2;
		if(target == arr[mid]) return mid;
		if((right - left) <= 0) return -1;
		if(target < arr[mid]) return doufin(arr, target, left, mid);
		else return doufin(arr, target, mid + 1, right);
	}

}

非递归

public int DoubleSearchNoRecursion(int []arr, int target) {
		int left = 0;
		int right = arr.length - 1;
		while(left <= right) {
			int mid = (left + right) / 2;
			if(arr[mid] == target) {
				return mid;
			}
			else if (target < arr[mid]) {
				right = mid - 1;
			}
			else {
				left = mid + 1;
			}
		}
		return -1;
	}

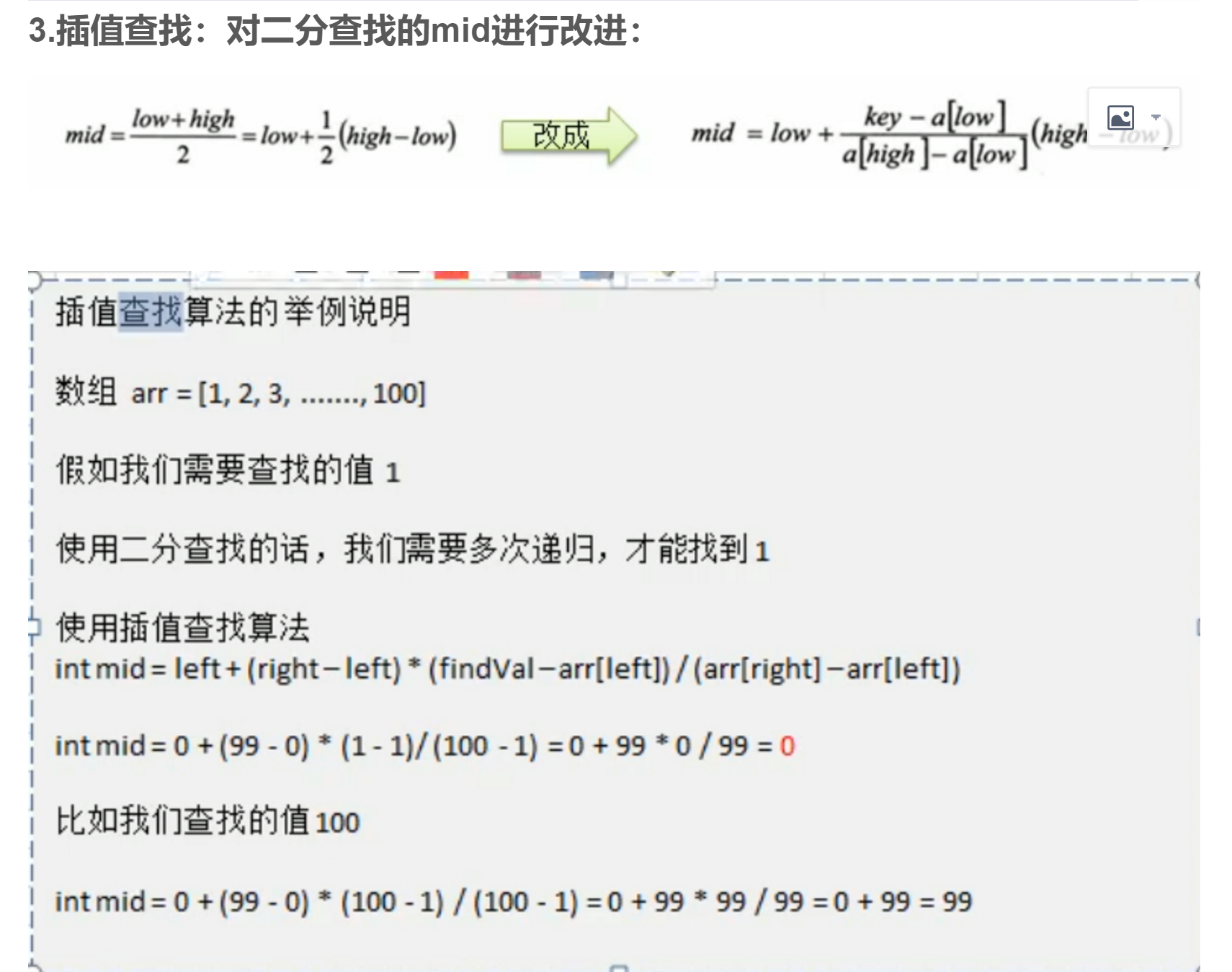
插值查找

斐波那契查找: 由于只有加减法运算，没有乘除，所以效率更高

原理是mid = fib（k - 1）-1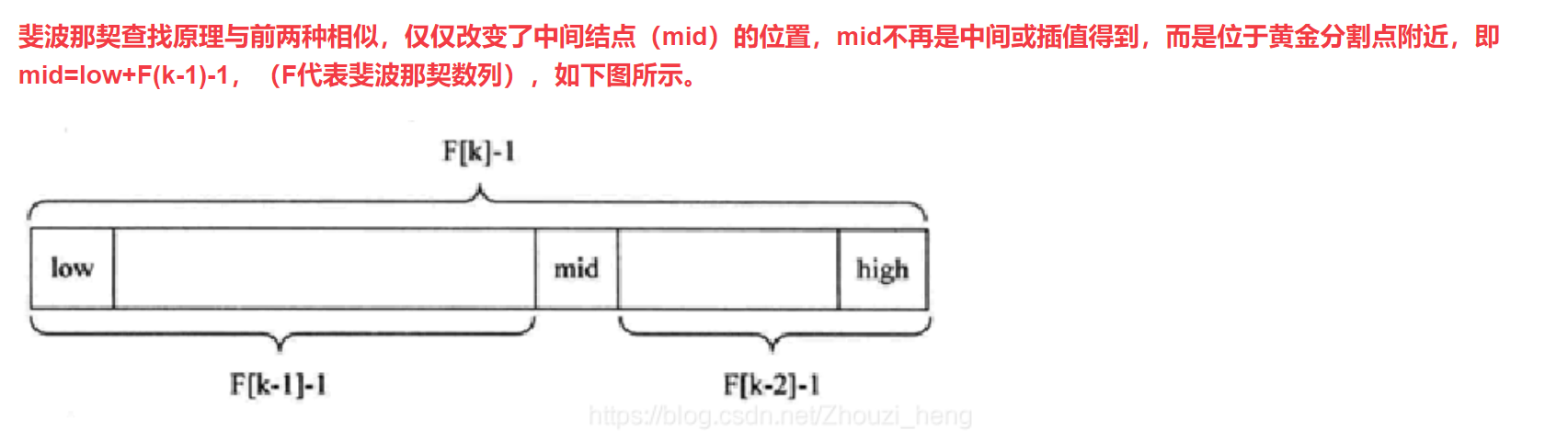

public class Fibonacci {
	public static int max = 20;
	public static int count = 0;
	public static int[] fib = new int[max];
	{
		fib[0] = 1;
		fib[1] = 1;
		for(int i = 2; i < max;i++) {
			fib[i] = fib[i - 1] + fib [i - 2];
		}
	}

	public static void main(String[] args) {
		Fibonacci f = new Fibonacci();
		int[] arr = new int[1000];
		for(int i = 0; i < arr.length; i++) {
			arr[i] = i;
		}
		//先用数组长度找到fibonacci数列的元素
		int k = 0;
		while(arr.length > fib[k]) {
			k++;
		}
		//使用arr的最后一位元素补齐arr
		int temp[] = new int [fib[k]];
		for(int i = 0; i < fib[k]; i++) {
			if(i < arr.length) temp[i] = arr[i];
			else {
				temp[i] = arr[arr.length - 1];
			}
		}
		//开始查找
		int result = fibSort(temp, 0, temp.length - 1, 444, k);
		if(result == -999) System.out.println(arr.length - 1);
		else System.out.println(result);
	}
	public static int fib(int n) {
		return fib[n];
	}
	public static int fibSort(int arr[], int left, int right, int target, int k) {
		System.out.println("执行----" + ++count);
		if(target == arr[right]) return -999;//由于查找到的是最后一位，由于补齐，比较麻烦，直接返回输出
		if((right - left) <= 0) return -1;
		int mid = left + fib[k -1] - 1;
		if(arr[mid] == target) return mid;
		//这边k -1 和 k -2 是因为fib(k) = fib(k-1) + fib(k-2)
		if(target < arr[mid]) return fibSort(arr, left, mid, target, k - 1);
		else {
			return fibSort(arr, mid + 1, right, target, k - 2);
		}
	}

}