Ch08 Tree
Yang Haoran 7/22/2019 Data structure
前序遍历:根节点,左子树,右子树
中序遍历:左子树,根节点,右子树
后序遍历:左子树,右子树,根节点
# 遍历,删除,查询方法:
public class OrderSearch {
public static void main(String[] args) {
Node root = new Node(0, "root");
Node a = new Node(1, "a");
Node b = new Node(2, "b");
Node c = new Node(3, "c");
Node d = new Node(4, "d");
BinaryTree tree = new BinaryTree(root);
root.left = a;
root.right = b;
b.left = c;
b.right = d;
tree.postOrder();
}
}
//定义一个二叉树
class BinaryTree{
Node root;
public BinaryTree(Node root) {
super();
this.root = root;
}
public void preOrder() {
if(root != null) root.preOrder();
else System.out.println("null");
}
public void postOrder() {
if(root != null) root.postOrder();
else System.out.println("null");
}
public void midOrder() {
if(root != null) root.midOrder();
else System.out.println("null");
}
}
//定义节点类
class Node{
int id;
String name;
Node left;
Node right;
public Node(int id, String name) {
super();
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "Node [id=" + id + ", name=" + name + "]";
}
//前序遍历
public void preOrder() {
System.out.println(this);
if(this.left != null) this.left.preOrder();
if(this.right != null) this.right.preOrder();
}
//中序遍历
public void midOrder() {
if(this.left != null) this.left.midOrder();
System.out.println(this);
if(this.right != null) this.right.midOrder();
}
//后序遍历
public void postOrder() {
if(this.left != null) this.left.postOrder();
if(this.right != null) this.right.postOrder();
System.out.println(this);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
# 顺序存储二叉树:把数组按照完全二叉树来存储,一层一层往下
- 左子节点为:2*index + 1
- 右子节点为:2*index + 2
- 父节点为:(index - 1)/ 2
public class OrderTree {
public static void main(String[] args) {
int[] arr = new int[] {1,2,3,4,5,6,7,8};
preOrder(arr, 0);
}
//顺序遍历输出
public static void preOrder(int[] arr, int index) {
if(arr.length == 0 ) System.out.println("数组为空");
//先输出根节点
int p = index;
System.out.println(arr[p]);
if((2 * p + 1) < arr.length) {
//递归左边
preOrder(arr, 2 * p + 1);
}
if((2 * p + 2) < arr.length) {
//递归右边
preOrder(arr, 2 * p + 2);
}
}
}
class ArrayNode {
int num;
ArrayNode left;
ArrayNode right;
public ArrayNode(int num) {
super();
this.num = num;
}
@Override
public String toString() {
return "ArrayNode [num=" + num + "]";
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
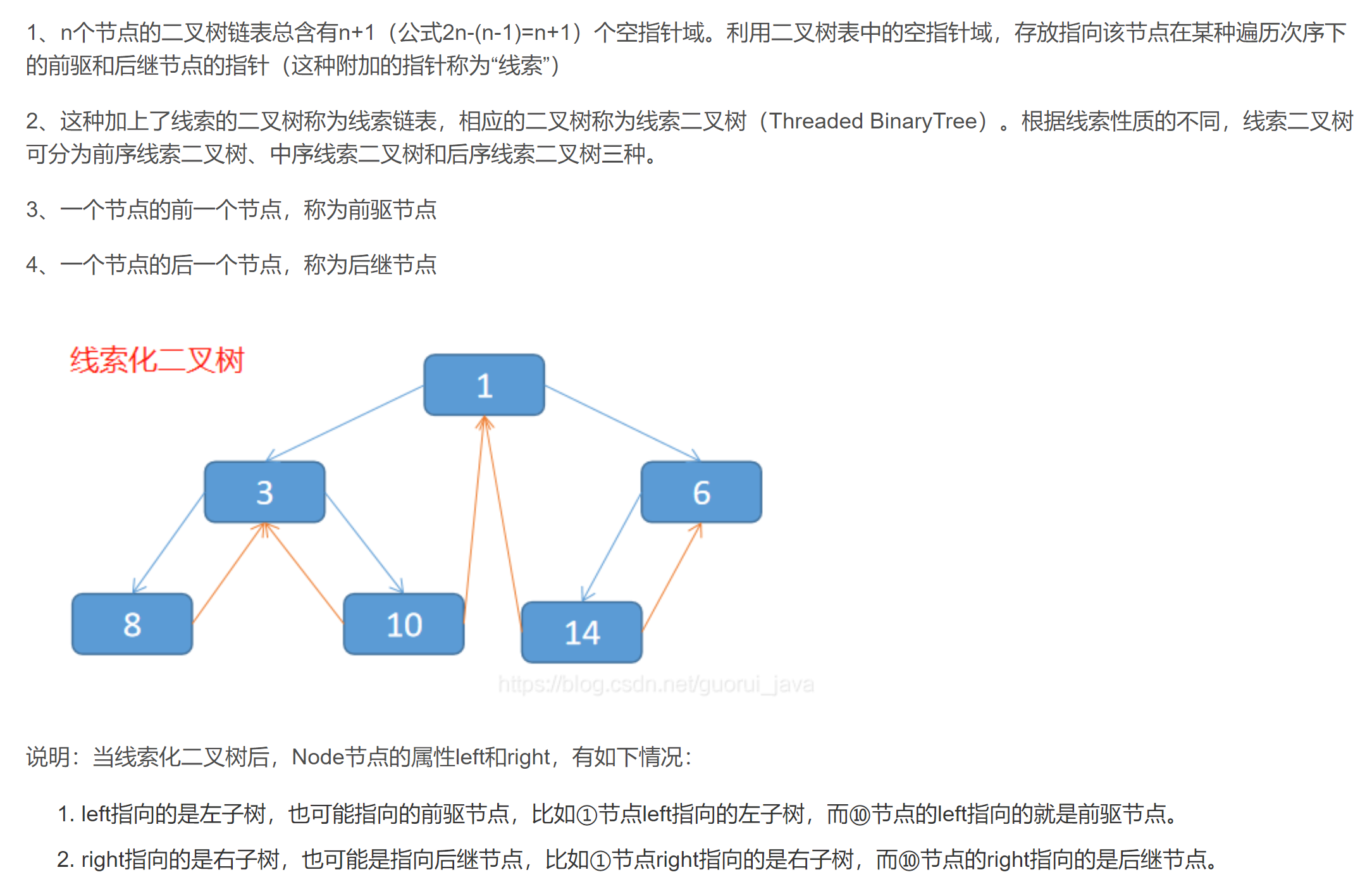
# 线索化二叉树:n个节点的二叉树中有2n-(n-1) = n + 1个空指针域,利用空指针指向上一个要遍历的节点(前驱)下一个要遍历的节点(后继),叫做线索
所以有前序线索化二叉树,中序线索化二叉树,后序线索化二叉树
//中序线索化二叉树
public void threaded(Node node) {
if(node == null) return;
//线索化左子树
threaded(node.left);
//线索化本节点
//左节点
if(node.left == null) {
node.left = pre;
node.leftType = 1;
}
//右节点(这边判断pre是防止空指针异常)
if(pre != null && pre.right == null) {
pre.right = node;
pre.rightType = 1;
}
//关键一步
pre = node;
//线索化右子树
threaded(node.right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
使用线索化的方式遍历线索化二叉树
堆
- 大顶堆:每个元素比他的左右子树都大,但左右子树的顺序无所谓
- 小顶堆:每个元素都比他的左右子树都小,但左右子树的顺序无所谓
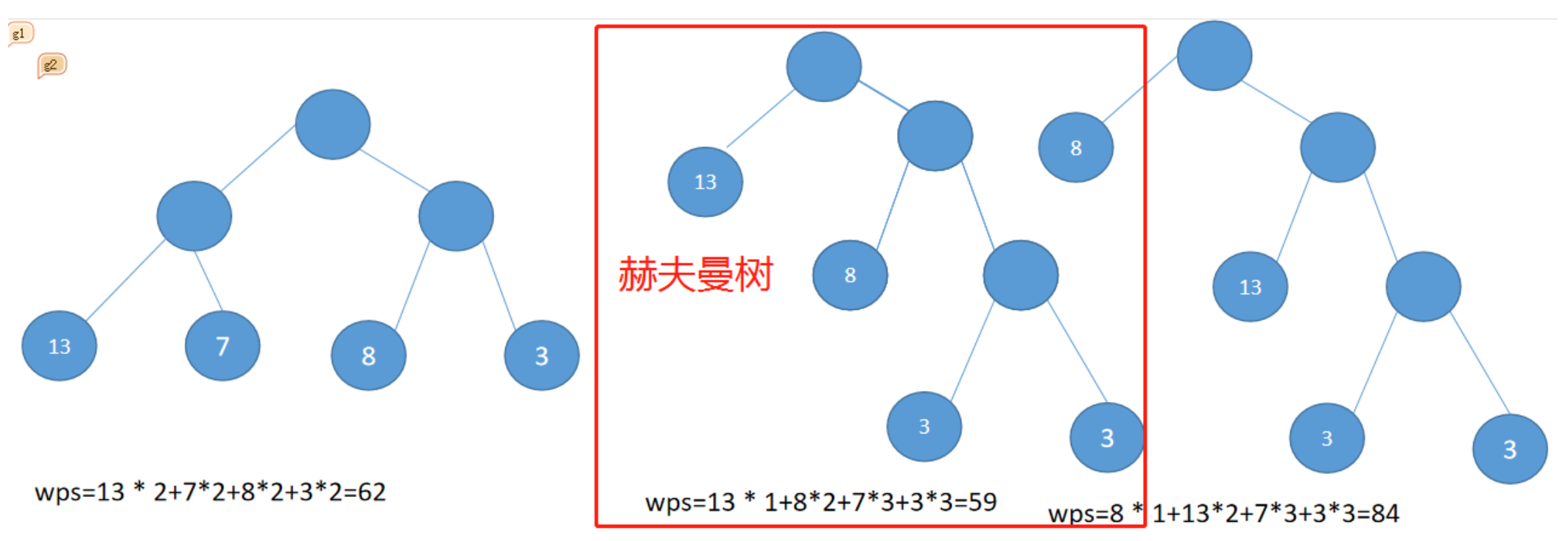
# 霍夫曼树
带权路径长度之和最小的树(∑结点的权 * 该结点到根节点的路径长度)
1、基本介绍 (1)给定n个权值作为n个叶子结点,构造一颗二叉树,若该树的带权路径长度wpl达到最小,称这样的二叉树为最优二叉树,也称为赫夫曼树。
(2)赫夫曼树是带权路径长度最短的树,权重较大的结点离根较近。
2、赫夫曼树几个重要概念和举例说明 (1)路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
(2)结点的权及带权路径长度
若将树中结点赋给一个有着某种意义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
(3)树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,为WPL(weighted path length),权重越大的结点离根结点越近的二叉树才是最优二叉树。
(4)WPL最小的就是赫夫曼树。
代码思路:
- 先把数组排序,取出前两个数,组成二叉树,根节点为这两个数之和
- 再把根节点放到数组里,排序,以此类推
- 返回根节点
public class Huffman {
public static void main(String[] args) {
int[] arr = new int[] {1,3,6,13,29,7,8};
Node node = huffman(arr);
System.out.println(node.value);
pre(node);
}
public static Node huffman(int arr[]) {
List<Node> list = new ArrayList<Node>();
//先把所有数变成节点,放到list中
for(int i = 0 ; i < arr.length; i++) {
list.add(new Node(arr[i]));
}
while(list.size() > 1) {
//排序
Collections.sort(list);
//把前两个区数取出来
Node left = list.get(0);
Node right = list.get(1);
//创建一个父节点
Node parent = new Node(left.value + right.value);
parent.left = left;
parent.right = right;
//删除原来的节点,把父节点放到list中
list.remove(left);
list.remove(right);
list.add(parent);
}
return list.get(0);
}
public static void pre(Node node) {
if(node != null) node.preOrder();
else {
System.out.println("empty");
}
}
}
class Node implements Comparable<Node>{
int value;
Node left;
Node right;
public Node(int value) {
super();
this.value = value;
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
@Override
public int compareTo(Node o) {
return this.value - o.value;
}
public void preOrder() {
System.out.println(this);
if(this.left != null) this.left.preOrder();
if(this.right != null) this.right.preOrder();
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

# 二叉排序树
左子<自己<右子
中序遍历刚好是排好序的
package binaryTree;
//二叉排序树
public class BinarysortTree {
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
int[] arr = new int[] { 7, 3, 10, 12, 5, 1, 9, 2,6 };
for (int i = 0; i < arr.length; i++) {
tree.add(new Node(arr[i]));
}
tree.midscan();
System.out.println();
tree.remove(7);
tree.remove(3);
tree.remove(10);
tree.remove(12);
tree.remove(5);
tree.remove(1);
tree.remove(9);
tree.remove(2);
tree.remove(6);
tree.midscan();
}
}
//二叉排序树
class BinarySearchTree {
private Node root;
public void add(Node node) {
if (root == null) {
root = node;
} else {
root.add(node);
}
}
public void midscan() {
if(root == null) {
System.out.println("null");
return;
}
root.midscan();
}
public void remove(int value) {
if (root == null) {
return;
}
Node remove = root.find(value);// 要被删除的节点
Node parent = root.findparent(value);// 要被删除德电节点的父节点
// 删除的是叶子节点
if (remove != null && parent != null && remove.left == null && remove.right == null) {
if (parent.left != null && parent.left.value == value) {
parent.left = null;
return;
} else if (parent.right != null && parent.right.value == value) {
parent.right = null;
return;
} else {
System.out.println("error");// 父节点不存在子节点
}
}
// 有两个子树的节点
else if (remove != null && parent != null && remove.left != null && remove.right != null) {
//注意!!!!把被删除节点的左子树提上来的话要提左子树的最大节点,以免跟删除节点的右子节点冲突,提右子树的话同理
remove.value = findmax(remove.left);
return;
}
// 有一个子树的节点
else if (remove != null && parent != null && (remove.left != null || remove.right != null)) {
// 要删除的节点为父节点的左节点
if (parent.left == remove) {
if (remove.left != null) {
parent.left = remove.left;
return;
} else {
parent.left = remove.right;
return;
}
}
// 要删除的节点为父节点的右节点
else {
if (remove.left != null) {
parent.right = remove.left;
return;
} else {
parent.right = remove.right;
return;
}
}
//删除跟节点
} else if (parent == null) {
System.out.println("删除根节点");
if(root.left != null) {
root.value = findmax(root.left);
}
else if(root.right != null) {
root.value = findmin(root.right);
}
else {
root = null;
}
}
}
//查找子树中最大的元素并删除
public int findmax(Node node) {
Node temp = node;
while(temp.right != null) {
temp = temp.right;
}
remove(temp.value);
return temp.value;
}
//查找子树中最小的元素并删除
public int findmin(Node node) {
Node temp = node;
while(temp.left != null) {
temp = temp.left;
}
remove(temp.value);
return temp.value;
}
}
class Node {
public int value;
public Node left;
public Node right;
public Node(int value) {
super();
this.value = value;
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
// 中序遍历
public void midscan() {
if (this.left != null) {
this.left.midscan();
}
System.out.println(this);
if (this.right != null) {
this.right.midscan();
}
}
// 添加节点
public void add(Node node) {
// 小于该节点
if (node.value < this.value) {
if (this.left == null) {
this.left = node;
} else {
this.left.add(node);
}
}
// 大于或等于该节点
else {
if (this.right == null) {
this.right = node;
} else {
this.right.add(node);
}
}
}
// 找到要删除的节点
public Node find(int value) {
if (this.value == value) {
return this;
} else if (value < this.value) {
return this.left.find(value);
} else {
return this.right.find(value);
}
}
// 找到要删除节点的父节点
public Node findparent(int value) {
if (this.left == null && this.right == null) {
return null;
}
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else if (value < this.value) {
return this.left.findparent(value);
} else if (value > this.value) {
return this.right.findparent(value);
} else {
return null;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
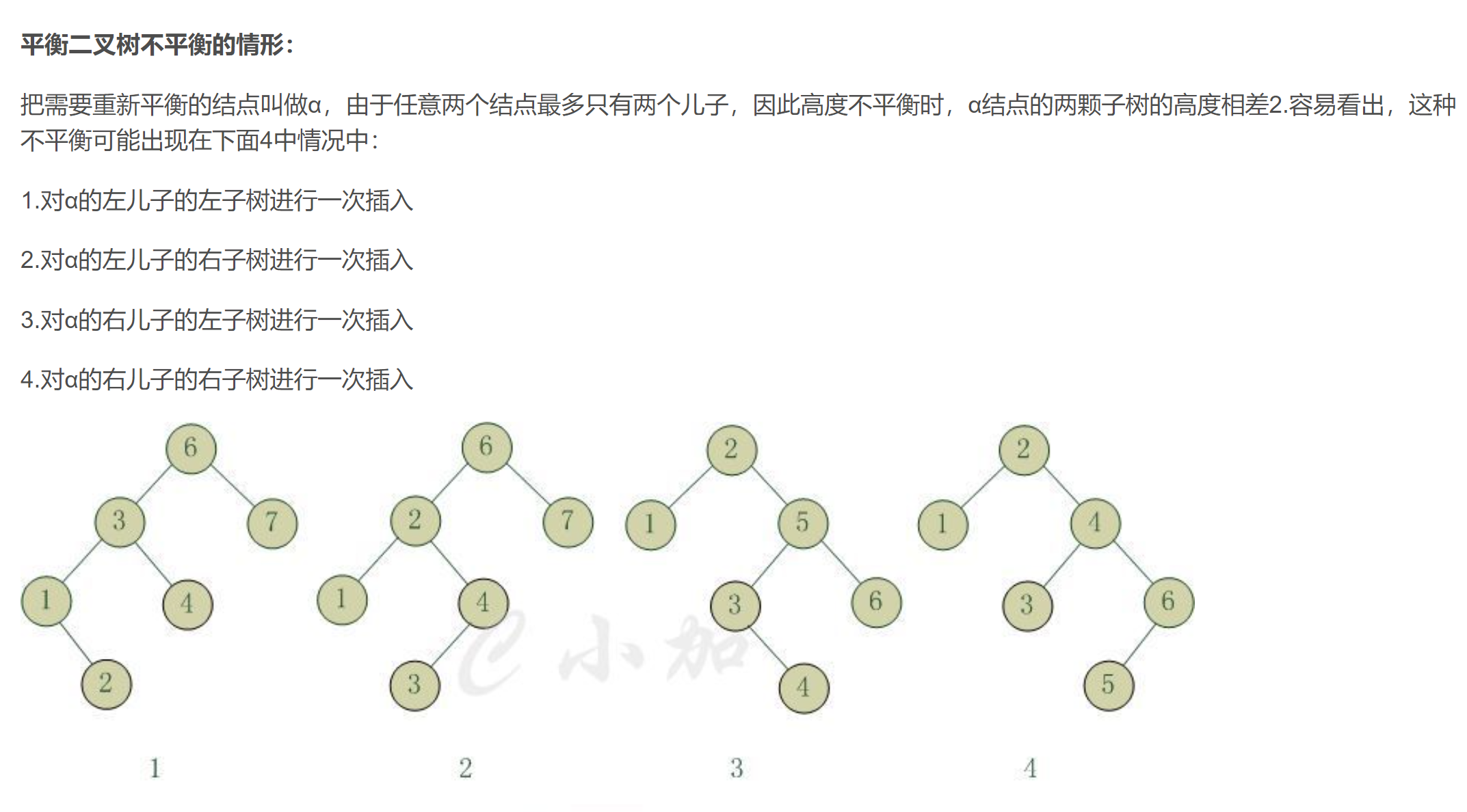
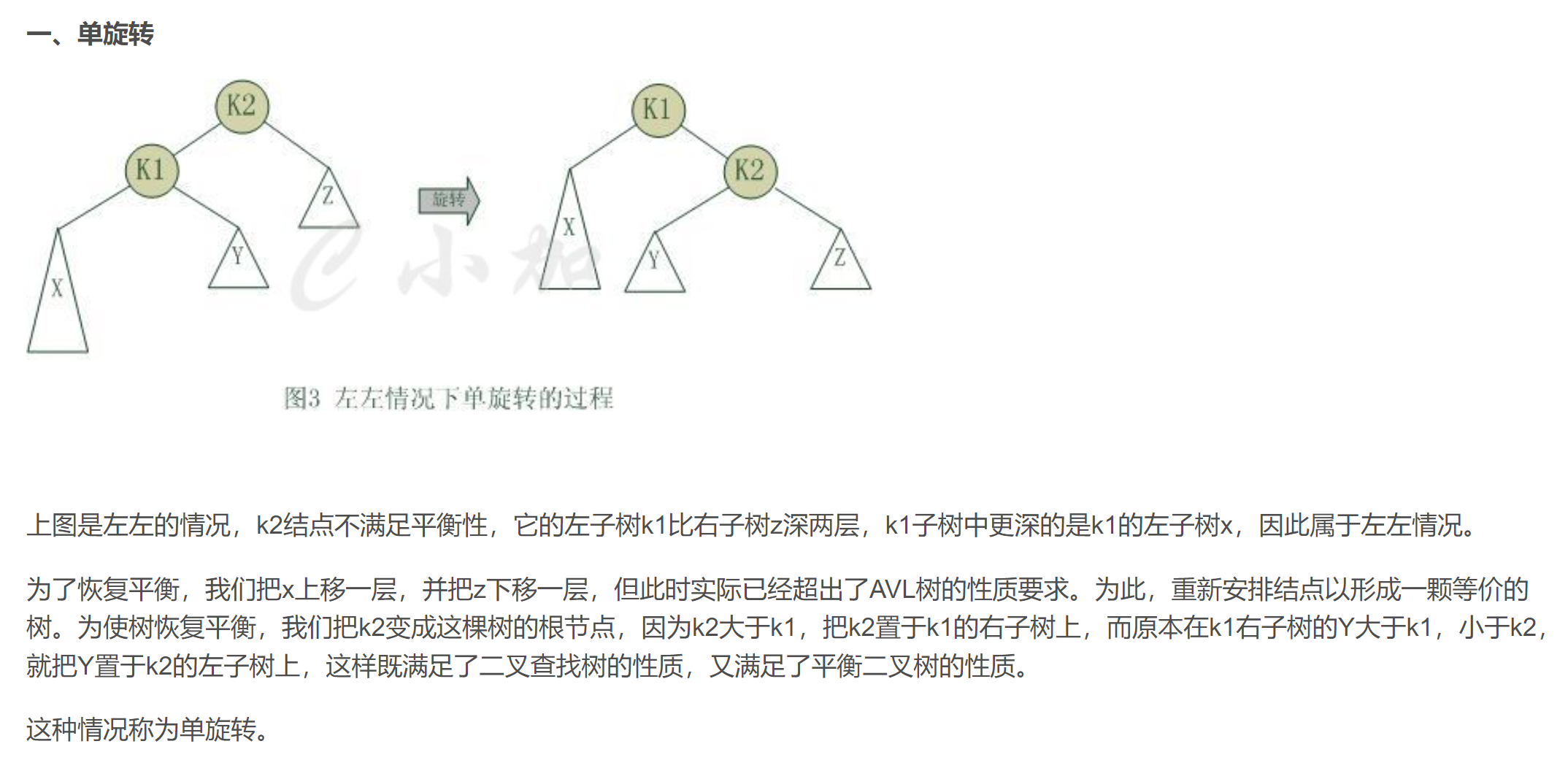
# AVL树(平衡二叉树)
包括红黑树,替罪羊树等等
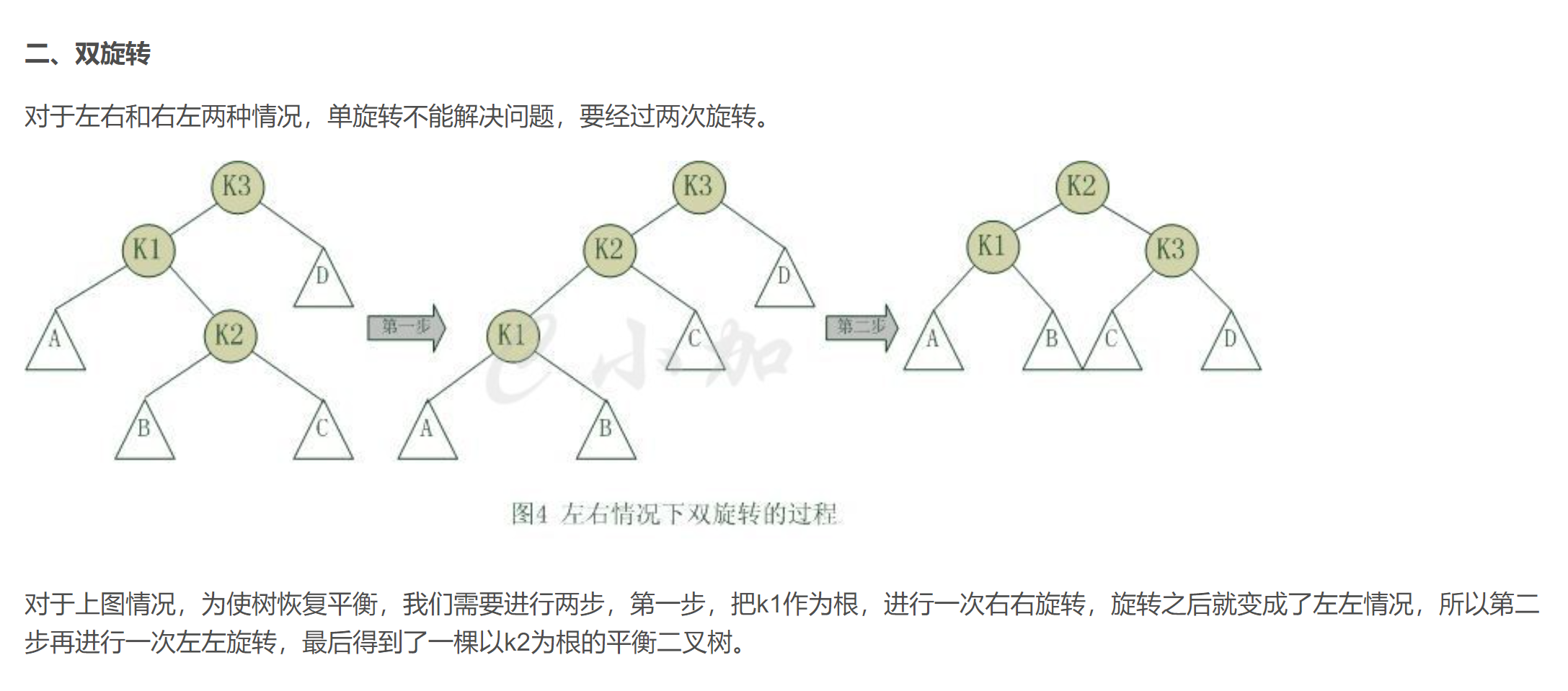

package AVLTree;
public class AVLTreeDemo {
public static void main(String[] args) {
int[] arr = new int[] {10,11,7,6,8,9};
AVLTree tree = new AVLTree();
for(int i = 0; i < arr.length; i++) {
tree.add(new Node(arr[i]));
}
tree.midscan();
int height = tree.height();
System.out.println(height + " left: " + tree.getRoot().leftheight() + " right: " + tree.getRoot().rightheight() + " root: " + tree.getRoot());
}
}
class AVLTree{
private Node root;
public Node getRoot() {
return root;
}
//返回树的高度
public int height() {
return root.hight();
}
public void add(Node node) {
if (root == null) {
root = node;
} else {
root.add(node);
}
}
public void midscan() {
if(root == null) {
System.out.println("null");
return;
}
root.midscan();
}
public void remove(int value) {
if (root == null) {
return;
}
Node remove = root.find(value);// 要被删除的节点
Node parent = root.findparent(value);// 要被删除的节点的父节点
// 删除的是叶子节点
if (remove != null && parent != null && remove.left == null && remove.right == null) {
if (parent.left != null && parent.left.value == value) {
parent.left = null;
return;
} else if (parent.right != null && parent.right.value == value) {
parent.right = null;
return;
} else {
System.out.println("error");// 父节点不存在子节点
}
}
// 有两个子树的节点
else if (remove != null && parent != null && remove.left != null && remove.right != null) {
//注意!!!!把被删除节点的左子树提上来的话要提左子树的最大节点,以免跟删除节点的右子节点冲突,提右子树的话同理
remove.value = findmax(remove.left);
return;
}
// 有一个子树的节点
else if (remove != null && parent != null && (remove.left != null || remove.right != null)) {
// 要删除的节点为父节点的左节点
if (parent.left == remove) {
if (remove.left != null) {
parent.left = remove.left;
return;
} else {
parent.left = remove.right;
return;
}
}
// 要删除的节点为父节点的右节点
else {
if (remove.left != null) {
parent.right = remove.left;
return;
} else {
parent.right = remove.right;
return;
}
}
//删除跟节点
} else if (parent == null) {
System.out.println("删除根节点");
if(root.left != null) {
root.value = findmax(root.left);
}
else if(root.right != null) {
root.value = findmin(root.right);
}
else {
root = null;
}
}
}
//查找子树中最大的元素并删除
public int findmax(Node node) {
Node temp = node;
while(temp.right != null) {
temp = temp.right;
}
remove(temp.value);
return temp.value;
}
//查找子树中最小的元素并删除
public int findmin(Node node) {
Node temp = node;
while(temp.left != null) {
temp = temp.left;
}
remove(temp.value);
return temp.value;
}
}
class Node {
public int value;
public Node left;
public Node right;
public Node(int value) {
super();
this.value = value;
}
//返回左子树的高度
public int leftheight() {
if(this.left == null) {
return 0;
}
else {
return this.left.hight();
}
}
//返回右子树的高度
public int rightheight() {
if(this.right == null) {
return 0;
}
else {
return this.right.hight();
}
}
//返回以当前节点为根节点的树的高度
public int hight() {
return Math.max(this.left == null ? 0 : this.left.hight(), this.right == null ? 0 : this.right.hight()) + 1;
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
// 中序遍历
public void midscan() {
if (this.left != null) {
this.left.midscan();
}
System.out.println(this);
if (this.right != null) {
this.right.midscan();
}
}
// 添加节点
public void add(Node node) {
// 小于该节点
if (node.value < this.value) {
if (this.left == null) {
this.left = node;
} else {
this.left.add(node);
}
}
// 大于或等于该节点
else {
if (this.right == null) {
this.right = node;
} else {
this.right.add(node);
}
}
//旋转操作
if(this.rightheight() - this.leftheight() > 1) {//右子树高
//右子树的左子树的高度大于右子树的右子树的高度
if(this.right != null && this.right.leftheight() > this.right.rightheight()) {
this.right.rightRotate();
this.leftRotate();
}
else {
this.leftRotate();
}
return;
}
if(this.leftheight() - this.rightheight() > 1) {//左子树高
//左子树的右子树的高度大于左子树的左子树的高度
if(this.left != null && this.left.rightheight() > this.left.leftheight()) {
this.left.leftRotate();
this.rightRotate();
}
else {
this.rightRotate();
}
return;
}
}
// 找到要删除的节点
public Node find(int value) {
if (this.value == value) {
return this;
} else if (value < this.value) {
return this.left.find(value);
} else {
return this.right.find(value);
}
}
// 找到要删除节点的父节点
public Node findparent(int value) {
if (this.left == null && this.right == null) {
return null;
}
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else if (value < this.value) {
return this.left.findparent(value);
} else if (value > this.value) {
return this.right.findparent(value);
} else {
return null;
}
}
//左旋转(右子树高度-左子树高度>1)
public void leftRotate() {
//先创建一个节点,跟当前节点一样
Node node = new Node(this.value);
//该节点的左节点连接到新节点的左节点
node.left = this.left;
//找到右子树的左子树,连接到新节点的右节点
node.right = this.right.left;
//该节点的右节点的左节点设置为新建节点
this.left = node;
this.value = this.right.value;
this.right = this.right.right;
}
//右旋转
public void rightRotate() {
Node node = new Node(this.value);
node.right = this.right;
node.left = this.left.right;
this.value = this.left.value;
this.left = this.left.left;
this.right = node;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
